Астрономия из первых рук

Космические миражи

В.М.Сидоров

Можно ли представить себе телескоп космических размеров в десятки, сотни и более килопарсеков? Если иметь ввиду рукотворные телескопы, то, пожалуй, трудно. Между тем, природа изготовляет такие “инструменты”. Речь идет о гравитационных линзах, целом классе астрономических объектов, недавно открытых и притягивающих к себе внимание исследователей. Слов нет, гравитационные линзы — объекты интересные, даже необыкновенные, но ничего сверхестественного в них нет. Физические принципы гравитационного линзования сравнительно просты и давно известны. Главный из них — взаимодействие гравитационного поля с излучением произвольной природы. В более конкретной форме он проявляется в искривлении траекторий любых частиц в поле тяготения. Наиболее последовательно этот принцип отражен в общей теории относительности (ОТО), появление которой на свет и послужило, по-существу, отправной точкой исследований по гравитационной фокусировке. Уже в 1915 г. благодаря работам Эйнштейна была выяснена роль гравитации в искривлении траекторий световых лучей, что и дало возможность Лоджу в 1919 г. и Эддингтону в 1920 г. опубликовать первые работы по гравитационной фокусировке электромагнитного излучения. Затем вплоть до открытия Уолшем, Карсвеллом и Вейманном в 1979 г. первой гравитационнолинзовой системы 0957+561(А,В), эти исследования носили сугубо теоретический характер и были всего лишь экзотикой. Суть открытия 1979 г. состояла в том, что на основании тождества спектральных характеристик и красных смещений тесной пары квазаров 0957+561 (А,В) с угловым расстоянием друг от друга 6", наблюдатели предположили возможность существования вместо разных квазаров двух изображений одного и того же квазара, т.е. двух "миражей". Это предположение вскоре было подкреплено сильным аргументом - на расстоянии 0,8" от компонента В была обнаружена гигантская эллиптическая галактика, которая была интерпретирована как гравитационная линза, создающая два изображения источника. Теоретическая экзотика стала обретать, наконец, реальную наблюдательную основу. Следствием открытия первой гравитационной линзы был взрыв активности исследователей, вызванный стремлением астрономов увидеть этот диковинный объект своими глазами и как можно полнее его исследовать. И практически сразу после открытия начались энергичные поиски новых аналогичных объектов. После того, как первые страсти улеглись, на смену энтузиазму пришли специальные, глубоко обоснованные программы поисков и исследований гравитационных линз, для реализации которых были использованы лучшие современные инструменты-телескопы и радиотелескопы. В итоге к сегодняшнему дню открыто более трех десятков гравитационных систем, разнообразных по своей структуре, причем большинство из них является пока кандидатами на роль этих объектов. По морфологическому признаку все гравитационные линзы можно разбить на три следующие группы: 1. Гравитационные линзы создающие кратные изображения, число которых сегодня наибольшее; 2. Гигантские светящиеся дуги — вторая по численности группа; 3. Кольцеобразные структуры, так называемые "кольца Эйнштейна". Все миражи, создаваемые представителями этих групп, формируются огромными массами порядка масс галактик, скоплений галактик (макролензинг). К гораздо более слабым наблюдательным эффектам приводят гравитационные линзы с массами порядка звезд (микролензинг), их действие может проявляться, например, в вариациях блеска источников. Точное число гравитационных линз вряд ли сейчас может быть названо, так как многие из этих объектов следовало бы отнести скорее к разряду кандидатов в кандидаты. За этой игрой слов скрывается всего лишь плохое знание природы объектов.

Другой хороший показатель активности работы астрофизиков - число научных публикаций. В соответствии с этим показателем подавляющая часть работ по гравитационному линзированию (более 3/4) приходится на сравнительно небольшой отрезок времени - после 1979 г.

Чем вызван такой интерес к гравитационным линзам и что эти объекты могут дать астрофизикам? Роль "космического телескопа" как мощного инструмента исследования Вселенной была отмечена Ф. Цвикки еще в 1937 г. Сегодня эта роль гравитационных линз осознана гораздо полнее и конкретнее. Во-первых, гравитационные линзы могут значительно усиливать излучение источников, с их помощью можно получать такую информацию об источниках, которую трудно было бы добыть другими способами. Во-вторых, изображения, созданные гравитационными линзами, содержат сведения, необходимые, для построения моделей самих линз (в первую очередь галактик). Такую информацию можно использовать в силу универсального характера гравитационного поля для моделирования распределения плотности вещества любого происхождения, в частности распределений скрытой массы (по некоторым оценкам она составляет от 90% до 97% полной массы Вселенной). В третьих, из анализа изображений источников, созданных гравитационными линзами, можно получать сведения об усредненных, крупномасштабных свойствах Вселенной, о таких космологических величинах как параметр Хаббла Н (соответствующее ему время t - возраст Вселенной), параметр замедления q и космологическая постоянная . Кроме того, такие "призраки Вселенной" как черные дыры и космические струны, непосредственно не наблюдаемые, но обладающие сильными гравитационными полями, также должны действовать на излучение как специфические гравитационные линзы. Обнаружение и исследование таких линз может пролить свет на некоторые фундаментальные проблемы астрофизики. Этим не исчерпываются, конечно, все возможности гравитационных линз в настоящее время. Что касается перспектив использования "космических телескопов", то о многом мы сейчас можем даже не догадываться, точно так же как не подозревал о нынешних возможностях телескопов Галилей, создавая свои инструменты.

Преломление световых лучей в поле тяготения

Физической основой гравитационного линзирования, как уже упоминалось, является эффект искривления траекторий частиц гравитационным полем. Каких конкретно частиц - не имеет значения ввиду универсального характера гравитационного поля, согласно которому все тела, независимо от их массы, должны двигаться в таком поле одинаково. Это свойство гравитационного поля является экспериментальным фактом, положенным в основу общей теории относительности. Прекрасным пособием для желающих познакомиться с основами ОТО может служить книга П. Бергмана "Загадка гравитации" (Изд. "Наука", Москва, 1969 г.). Таким образом, гравитационное поле в принципе способно искривлять траектории движения, и, следовательно, фокусировать любые по своей природе объекты - от элементарных частиц до макроскопических тел. При этом элементарные частицы могут как обладать массой (электроны, протоны, нейтроны...), так и не иметь ее, точнее иметь равную нулю массу покоя (гравитоны, фотоны...). Нас будут интересовать исключительно световые потоки (фотоны) и воздействие на них гравитационного поля, создаваемого различными астрономическими объектами - линзами: звездами, галактиками, скоплениями галактик.

Впервые эффект искривления траекторий световых лучей в гравитационном поле был экспериментально проверен в 1919 г. Во время полного солнечного затмения английский астроном А. Эддингтон измерил координаты звезд вблизи солнечного диска в полной фазе затмения, когда влияние Солнца наибольшее, и сравнил их с положением тех же звезд, когда искажающее воздействие Солнца практически отсутствует. По разнице координат двух положений звезд Эддингтон определил величину эффекта 1,98". В пределах небольшой ошибки этот результат соответствовал выводам ОТО, т.е. величине 1,75", что являлось первым экспериментальным подтверждением релятивистской теории. Однако для того, чтобы понять качественную сторону явления, совсем не обязательно прибегать к столь сложной теории - для этого вполне достаточно обратиться к обычной ньютоновской теории тяготения. Для этого необходимо сделать два предположения: 1. Согласно квантовому дуализму волне-частице электромагнитной волны с частотой n будем ставить в соответствие частицу (фотон) с эффективной массой m = hv/c²; 2. Фотон и некоторое макроскопическое тело с массой М взаимодействуют между собой по ньютоновскому закону тяготения:

Здесь введены обозначения: h - постоянная Планка, с - скорость света, G - гравитационная постоянная, r - расстояние между взаимодействующими объектами. Уже с самых первых шагов ньютоновского подхода могут появиться сомнения в правомерности его применения. Суть в том, что ньютоновская теория применима только для слабых гравитационных полей, между тем как из формулы (1) видно, что при уменьшении расстояния r величина силы взаимодействия F неограниченно возрастает (при r стремящемся к нулю F стремитсяся к бесконечности). Однако нетрудно оценить границу корректности ньютоновского подхода. Такая оценка основывается на том очевидном, наглядном факте, что траектория частицы тем более прямолинейна, чем больше ее начальная скорость и чем больше минимальное расстояние r_min от центра тяготения до частицы на ее траектории. На физическом языке это означает, что кинетическая энергия ньютоновской частицы (фотона) mc²/2 должна значительно превышать ее максимальную по абсолютному значению потенциальную энергию GMm/r_min. Отсюда следует неравенство

означающее, что траектория частицы не должна проходить близко от центра тяготения. Величина r_g = 2GM/c² носит название гравитационного радиуса тела. Рассмотрим в качестве примера ситуацию с траекторией фотона, проходящей вблизи края Солнца. Совершенно ясно, что Солнце непрозрачно для фотонов и, следовательно, их траектории должны иметь минимальное удаление от центра тяготения, равное радиусу Солнца . Гравитационный радиус Солнца, вычисленный по формуле (2), имеет значение r_g = 3 км. Таким образом, неравенство r_min = >> r_g надежно выполняется в нашем примере, как выполняется оно в большинстве случаев астрономической практики за исключением черных дыр. Хотя приведенные рассуждения и дают нам некоторые основания для применения ньютоновской теории, нужно не забывать, что ошибка при этом все же совершается. Какая конкретно, будет видно из дальнейшего. Здесь уместно напомнить, что представления, аналогичные современным, о гравитационном радиусе и черных дырах только в других терминах, были впервые введены в физику Лапласом в конце XVIII в. Основывая свои вычисления на ньютоновской теории, он пришел к выводу, что звезды с достаточно большими плотностью и размерами своим притяжением не должны "отпускать свет наружу", т.е. становятся невидимыми для внешнего наблюдателя. Основываясь на законах ньютоновской физики вне области их применения, он тем не менее пришел к правильному выводу.

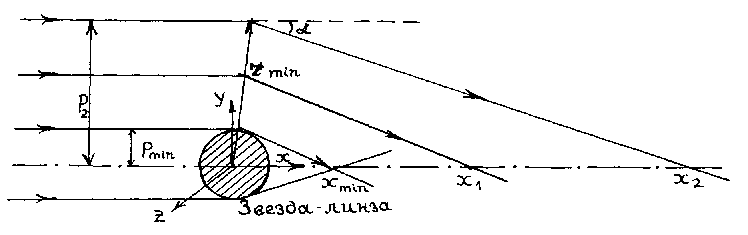
(Рис. 1 Отклонение фотонов в гравитационном поле звезды.)

Рассмотрим непрозрачную гравитационную линзу и налетающий на нее световой поток от очень удаленного источника, вследствии чего приходящие к линзе лучи можно считать практически параллельными (рис. 1). Поместим начало системы координат в центр тяготения так, чтобы ось x совпадала с направлением распространения световых лучей.

Возьмем максимально простое распределение плотности вещества в гравитационной линзе, т.е. будем считать плотность постоянной по всему объему линзы: p= const. Такой объект будет порождать сферически-симметричное гравитационное поле, поэтому его потенциал и сила взаимодействия будут зависеть только от расстояния r. В таком симметричном поле движение каждой частицы будет происходить в определенной плоскости, поэтому одну из координат можно вообще исключить из рассмотрения (например, координату z) - на рис. 1 траектории фотонов изображены в плоскости (x, y). Радиус-вектор частицы будет также зависеть от двух координат:r²=x²+y² . Важнейшей характеристикой гравитационной линзы является угол отклонения световых лучей a, образуемый пересечением двух асимптот к приходящему и уходящему от линзы лучам (рис. 1), и его зависимость от прицельного параметра Р. Так принято называть минимальное расстояние от центра тяготения до траектории частицы, если бы эта траектория не была искривленной. Уже сам характер взаимодействия частицы с гравитационными линзами наталкивает на мысль о том, что угол a должен обратно пропорционально зависеть от прицельного параметра, т.е. с увеличением Р угол отклонения a должен уменьшаться. Однако более строгую, конкретную зависимость можно найти, решив ньютоновские уравнения движения фотона в гравитационном поле линзы:

(3)

Процедура решения этих простых уравнений не входит в наши намерения, однако отметим основные этапы на пути к интересующему нас результату. Решением уравнения движения (3) мы определяем сначала траекторию фотона, затем определяем асимптоты восходящей и нисходящей ветвей этой траектории и, наконец, по асимптотам находим зависимость a(Р):

(4)

Оценим величину угла для конкретного примера траектории фотона, касающейся края Солнца. При r_g > 3 км и P = км получим:

(5)

Эта величина оказалась приблизительно вдвое меньше измеренной Эддингтоном во время солнечного затмения. Гораздо лучшее соответствие с экспериментом дает релятивистская теория (ОТО). Согласно представлениям этой теории, гравитационное поле проявляется через геометрические свойства четырехмерного риманова пространства-времени, важнейшим из которых является его кривизна. Наиболее простым и наглядным примером двумерного искривленного (риманова) пространства является поверхность шара. В свою очередь геометрические свойства пространства-времени непосредственно зависят от распределения материи. Таким образом, в ОТО, как и в ньютоновской теории тяготения, существует прямая зависимость свойств гравитационного поля от его источников. Однако, в отличие от теории Ньютона, в ОТО и само гравитационное поле воздействует на распределение материальных источников и их движение, что приводит к нелинейному характеру уравнений тяготения и значительным осложнениям при их анализе. Движение всех тел в римановом пространстве-времени происходит по так называемым геодезическим траекториям - кратчайшим экстремальным линиям, соединяющим две заданные точки. Примером таких геодезических линий в искривленном двумерном пространстве могут служить кривые, образуемые пересечением поверхности сферы с плоскостями, проходящими через ее центр. Любые нецентральные сечения уже не будут давать геодезических линий и, следовательно, приводят к более длинным расстояниям между двумя точками. А то, что две произвольные точки поверхности сферы всегда можно соединить геодезической, ясно в нашем примере уже из того, что через три точки (две на поверхности сферы и одну центральную) всегда можно провести плоскость, причем только одну, что и приводит к однозначному решению задачи.

Рассмотрим, как и в ньютоновском случае, движение фотонов в гравитационном поле однородного шара, но уже с точки зрения релятивистской теории. Как и прежде, гравитационное поле такого шара обладает сферической симметрией, и движение фотонов в нем будет плоским, т.е. должно происходить в определенной плоскости, однако их траекториями в этом случае теперь будут геодезические линии. Для получения зависимости угла преломления a от прицельного параметра Р теперь необходимо решать уравнения геодезических линий, гораздо более сложные, чем ньютоновские уравнения движения (3), хотя основные этапы получения результата (уравнения - траектория - асимптоты - угол отклонения) остаются теми же, что и прежде. Формула для угла отклонения света в релятивистской теории была впервые получена Эйнштейном в 1915 г. и, несмотря на более трудные подходы к ней, так же проста, как и формула (4):

(6)

отличаясь от нее двойкой в числителе. Соответственно, в два раза большим будет численное значение угла отклонения луча света от звезды, проходящего у края Солнца:

(7)

Полученная величина хорошо согласуется с наблюдениями, так что этот факт является одной из тех экспериментальных основ, на которые опирается релятивистская теория.

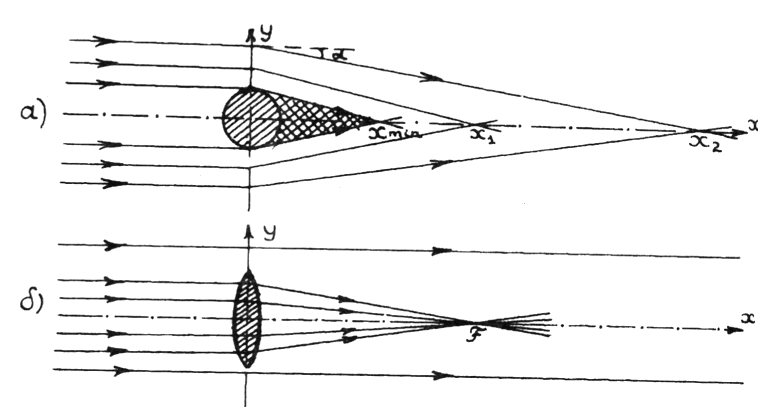
Формула (6), при всей ее простоте, уже дает возможность сделать некоторые выводы о характере рассматриваемой гравитационной линзы. Центральная симметрия гравитационного поля приводит к тому, что все лучи, имеющие один и тот же прицельный параметр сойдутся в одной точке (фокусе) на оптической оси - оси X (рис. 2а). Расстояние этой точки от центра гравитационной линзы легко оценить, приняв во внимание формулу (6) и очевидное геометрическое равенство , справедливое при малых значениях угла отклонения a (напомним, что углы малы при условии P = R >> r_g).

Из этих двух соотношений получаем простую зависимость:

(8)

из которой следует, что гравитационная линза имеет множество фокальных точек. Для большей наглядности будем проводить параллель между свойствами гравитационных линз и собирательными оптическими линзами. В отличие от обратной зависимости угла преломления от прицельного параметра для гравитационной линзы, как это видно из формулы (6), в случае оптической линзы действует прямая зависимость:

(9)

Если оптическая линза (без учета аббераций - искажений) собирает в одном фокусе F пучок лучей с разными значениями прицельного параметра (рис. 2б), то фокальные точки гравитационной линзы заполняют собой полуось . Это означает, что фокусные расстояния принимают значения от минимальной величины

определяемой из формулы (8) при условии P = R до бесконечности при Р стремящемся к бесконечности (рис. 2а). Значения X от R до F_min определяют область тени гравитационной линзы, заштрихованную на рис. 2а. Совершенно ясно, что такое устройство фокальной полуоси возможно только для непрозрачных линз (например, звезд). В тех случаях, когда вещество гравитационной линзы не является препятствием для излучения и линзы прозрачны (это либо те же звезды для гравитонов и нейтрино, либо галактики для фотонов), зависимость угла отклонения от прицельного параметра внутри гравитационной линзы будет уже несколько более сложной, чем для ее внешних областей:

(10)

хотя внешний вид этого соотношения мало отличается от формулы (6). В данном случае в гравитационный радиус r_g входит не полная масса шара М, как раньше, а только его часть, заключенная в цилиндре радиуса Р, вырезаемого из объема шара излучением:

(11)

Нетрудно показать на простом примере однородного шара, что свойства такой гравитационной линзы при небольшом значении прицельного параметра Р (Р << R) эквивалентны свойствам обычной собирательной оптической линзы. Световые лучи в этом примере, так же как и в оптической линзе, будут собираться в одном фокусе F, а зависимость угла преломления для таких лучей от прицельного параметра будет прямой, как в оптической линзе, т.е. будет выражаться формулой (9). Если читателю будет интересно, он без особого труда сможет рассчитать фокусное расстояние F такой гравитационной линзы, не забывая условие Р << R. При этом заранее ясно, что фокусное расстояние должно зависеть от параметров гравитационной линзы, таких как ее радиус и плотность. Таким образом, оптические свойства рассмотренной прозрачной линзы изменяются от свойств простейшей гравитационной линзы в ее внешней области , где гравитационное поле однородного шара тождественно полю точечной массы М, равной массе шара, до характеристик собирательной оптической линзы в приосевой зоне.

Как возникают миражи

Модель гравитационной линзы в виде однородного шара, конечно, была весьма упрощенной и носила чисто иллюстративный характер. Реальные гравитационные линзы намного сложнее, сложность линз порождает многообразие их типов, а это приводит, в свою очередь, к разнообразию видов изображений. Если для решения одних задач оказывается достаточным приближение точечной массы гравитационной линзы, то при решении других приходится подгонять как можно ближе к реальности модели галактик-линз с ядрами, да еще с неоднородными и несимметричными (неизотропными) распределениями звезд в их объемах. Нередко возникает необходимость рассматривать скопления галактик (кластеры), играющие роль гравитационных линз. Может встретиться и экзотика - необъемное распределение плотности в космической струне-линзе с чудовищной линейной плотностью вещества p > 10¹⁹ г/см. Реальность может быть очень сложной, но основные принципы, лежащие в основе гравитационных линз сравнительно просты, что нелишне подчеркнуть еще раз. Легче всего они усваиваются на простых примерах, один из которых мы сейчас и рассмотрим. Конкретно попробуем разобраться в том, как гравитационная линза образует кратные изображения источников.

Представим себе следующую систему: наблюдатель с телескопом, простейшая гравитационная линза (точка или однородная сфера массы М) на расстоянии D₁ от наблюдателя и отдаленный точечный источник (например, квазар), расположенный на расстояниях D₂ от наблюдателя и D₃ от гравитационной линзы так, что выполняется условие линзы D₃ > D₁ (рис. 3). Кроме того, предположим, что источник не экранируется линзой, т.е. находится на достаточном удалении S от оси наблюдатель-линза. Заметим по этому поводу, что на практике совмещение на одной линии источника, гравитационной линзы и наблюдателя хотя и маловероятно, но все же возможно, и такой случай будет рассмотрен в дальнейшем.

Что может ожидать наблюдатель в такой ситуации? Во-первых, он зафиксирует некоторый луч 1, а вернее, пучок лучей, с прицельным параметром Р₁ (рис. 3). Этим лучам будет соответствовать изображение источника К₁, положение которого не будет совпадать с истинным его положением К на небесной сфере. На рисунке прицельным параметром Р₁ обозначено расстояние от центра тяготения до точки излома траектории, что на первый взгляд не соответствует определению этого параметра. Так оно и есть на самом деле, однако размер этого несоответствия составляет малую величину = r_g при r_g << P, а следовательно, большой ошибки мы здесь не совершаем. Во-вторых, напрашивается предположение, что к наблюдателю может прийти и другой пучок (луч 2), но уже с противоположной стороны гравитационной линзы (на рисунке с нижней) и другим прицельным параметром. Этот второй пучок лучей сформирует тогда второе изображение источника К₂, также отличающееся по своему местоположению от истинного. Таким образом, вместо одного источника наблюдатель, вероятно, увидит два миража К₁ и К₂. А теперь попробуем проверить расчетами наши предположения.

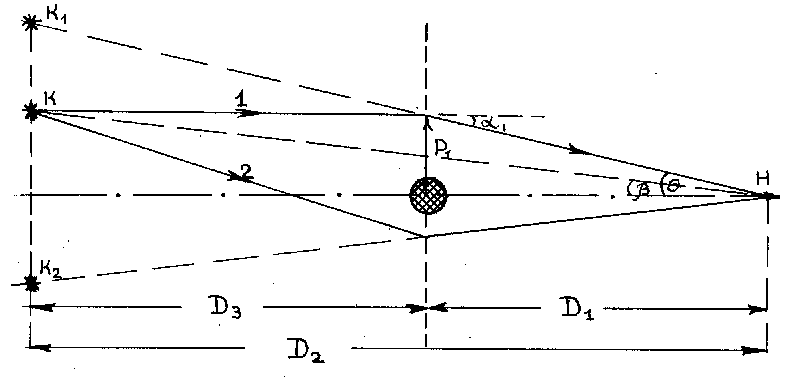
(Рис. 3 Образование миражей в поле тяготения массивной линзы.)

Для решения большого количества задач, возникающих при анализе гравитационно-линзовых систем аналогичных нашей, включая моделирование всевозможных ситуаций, астрофизики используют так называемые линзовые уравнения:

(12)

В левой части равенства величина S_p означает проекцию на плоскость гравитационной линзы расстояния S от источника до оси линза-наблюдатель (рисунок 3). Вывод этого уравнения несложен и основан на предположении малости углов отклонения, поэтому и применять его можно только при малых углах. Решить уравнение (12) применительно к нашей задаче значит определить из него все значения прицельного параметра Р при известных значениях остальных величин. С учетом формулы (6) линзовое уравнение приобретает более конкретный вид:

(13)

где D = D₁D₃/D₂ и приводится после простых преобразований к обыкновенному квадратному уравнению:

(14)

Пара корней этого уравнения:

(15)

дает нам все возможные значения прицельного параметра (Р₁, Р₂) лучей, приходящих в точку наблюдения. Следовательно, эти значения будут соответствовать двум изображениям с угловым расстоянием между ними . Здесь рассмотрен случай очень простой гравитационной линзы, более сложные примеры моделирования приведены в книге П. В. Блиоха, А. А. Минакова "Гравитационные линзы" (Киев, "Наукова думка", 1989 г.). Дадим еще одну наглядную геометрическую иллюстрацию полученного результата. Суть ее состоит в графическом анализе линзовых уравнений (13). По оси абсцисс будем откладывать значения прицельного параметра Р, а по оси ординат - две функции и , где a = 2Dr_g (рис. 4).

Функция задает прямую (на рисунке обозначено цифрой 1), J2 - гиперболу (график с цифрой 2). Значения прицельного параметра Р_A и Р_B, соответствующие точкам пересечения этих кривых, и будут решениями нашего уравнения. Таким образом, из графика мы быстро находим, во-первых, количество решений линзовых уравнений (число изображений) и, во-вторых, приблизительные значения прицельных параметров. Этим примером проиллюстрирован простейший случай точечной гравитационной линзы. Но эффективность графического метода на простом примере не очень ощущается, она резко возрастает при усложнении задачи - ведь в реальности могут встретиться гораздо более сложные распределения вещества в гравитационных линзах (а, следовательно, и гравитационного поля), в том числе не обладающие центральной симметрией. В таких случаях пришлось бы решать намного более сложные линзовые алгебраические уравнения третьего, четвертого и более высоких порядков. На рис. 4 представлен еще один пример более сложной, прозрачной гравитационной линзы (кривая 3). Три точки пересечения кривых и соответствуют решениям линзового уравнения третьего порядка и, следовательно, трем изображениям источника. В этом случае возможно пересечение графиков и в двух точках, когда в одной точке прямая касается кривой, а в другой - пересекает ее, однако такой случай является критическим. Это видно уже из того, что при малых сдвигах ("шевелениях") прямой две точки пересечения превращаются в три или в одну.

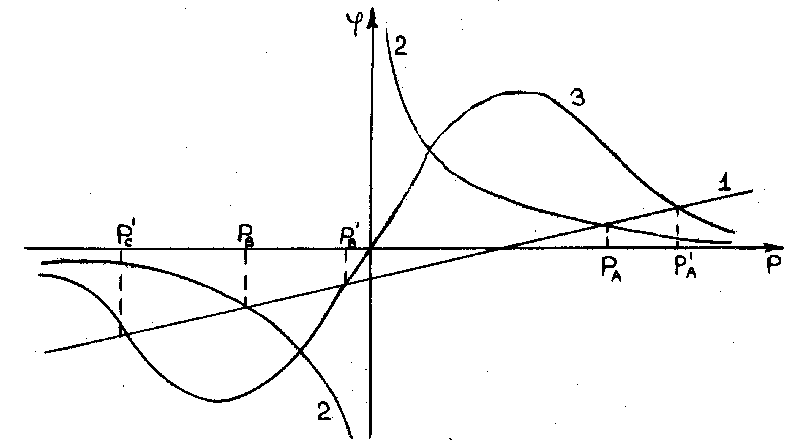
(Рис. 4 Три примера графического анализа линзовых уравнений.)

Описанное свойство гравитационных линз создавать кратные изображения принципиально отличает их от собирательных оптических линз, для которых также существуют линзовые уравнения. И хотя общий вид их идентичен уравнениям для гравитационных линз (12), однако закон преломления (9) придает оптическим уравнениям более простой вид:

(16)

Это уравнение устанавливает взаимно-однозначное соответствие между множеством значений величины Sp и множеством Р за исключением фокальных плоскостей линзы, где выполняется условие F = D. В свою очередь это означает единственность решения уравнения (16) при :

(17)

Такого соответствия (математики говорят "изоморфизма"), не существует в случаях гравитационных линз, где одному значению S_p может соответствовать несколько значений прицельного параметра Р.

Рассмотрим простой, но весьма интересный частный случай гравитационно-линзовой системы, когда источник, гравитационная линза и наблюдатель расположены на одной линии - комбинация, редко встречающаяся на практике. Такая ситуация также описывается линзовыми уравнениями (13), но при условии S_p = 0:

(18)

В этом случае картина, легко воспроизводимая по рис. 3, будет исключительно симметричной относительно оптической оси - лучи с данными значениями параметра Р будут приходить к наблюдателю по образующим конуса. Поэтому в свой телескоп он увидит кольцевое изображение источника ("кольцо Эйнштейна"), имеющее радиус:

(19)

Если гравитационная линза не является точечным объектом и к тому же непрозрачна, то наблюдатель сможет увидеть кольцо только при условии превышения его размеров радиуса линзы: P_k > R, а, следовательно, он должен находиться от центра линзы дальше некоторого минимального расстояния. Расчет этого расстояния несложен, так что читатель при желании всегда это сможет проделать, взяв за основу соотношение (19) и учтя условие P_k > R. Толщина такого кольцевого изображения будет бесконечно малой, так как мы рассматривали точечный источник. Если же источник имеет конечные размеры, например форму диска радиуса R*, то картина принципиально не изменится, т.е. кольцо сохранится, но будет иметь конечную ширину dР = R*D₁/D₂ (рис. 5а). По мере того, как источник будет смещаться от оптической оси, изображение начнет деформироваться.

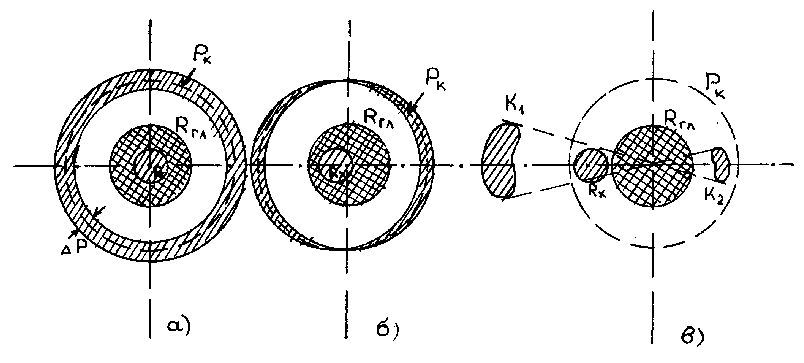
(Рис. 5 Изменение формы изображения источника радиуса R* по мере смещения его центра с оси наблюдатель-линза.)

Если он сместится на величину своего радиуса R*, то кольцо превратится в два серпа соединенных своими концами (рис. 5б). Если источник сместится от оси еще больше, то концы серпов разомкнутся - изображения превратятся в два изогнутых эллипса (рис. 5в). При значительном угловом удалении источника от гравитационной линзы ее влияние на изображении практически уже не будет сказываться, от двух изображений останется одно, а его форма станет копией формы источника, если не учитывать искажающего влияния оптических систем наблюдателя.

Гравитационные линзы не только искривляют траектории фотонов и создают причудливые изображения, они, кроме того, искажают энергетику излучения, изменяя распределение энергии световых потоков. Следствием этого может быть значительное усиление интенсивности приходящего к наблюдателю излучения. По-существу, это уже подразумевалось ранее, когда речь шла об особенностях фокальной полуоси гравитационной линзы, на которой происходит концентрация световой энергии. Усиление излучения принято характеризовать коэффициентом, представляющим собой отношение интенсивности светового потока I в точке наблюдения к интенсивности излучения I₀ в плоскости гравитационной линзы: q = I/I₀. В случае нескольких изображений суммарный коэффициент будет складываться из коэффициентов усиления для каждого компонента, в частности, при двух изображениях q = q₁+ q₂. Наблюдатель, расположенный на оптической оси со своим инструментом и рассматривающий изображение удаленного точечного источника (рис. 3), будет отмечать следующие изменения яркости изображений по мере смещения источника с оптической оси. В том случае, когда источник находится на самой оптической оси (S_p=0), наблюдатель зафиксирует бесконечное усиление яркости изображения (кольца). При смещении источника от оси на малую величину S (величину S_p в плоскости гравитационной линзы) изображение станет двойным, как нам уже известно, причем коэффициенты усиления каждого компонента будут уже конечными, хотя и очень большими. Изображения расположены с внутренней и внешней стороны кольца радиуса , при этом внешнее изображение обладает большей яркостью по отношению к внутреннему. По мере все большего удаления источника от оптической оси (S стремится к бесконечности) внешнее изображение все дальше будет отрываться от гравитационной линзы, а величина усиления его яркости q будет падать и стремиться к единице. Это означает, что на достаточном удалении от гравитационной линзы усиления яркости изображения не происходит. Одновременно с этим внутреннее изображение начнет приближаться к линзе (P₂ стремится к R, где R - радиус линзы) до тех пор, пока не будет ею заэкранировано, при этом коэффициент усиления внутреннего компонента будет стремиться к нулю (q₂ стремится к 0). В свою очередь, это будет означать, что второе изображение исчезнет из поля зрения наблюдателя. Принципиально картина не изменится и в случае большего числа изображений. Еще раз стоит подчеркнуть, что отмеченная особенность гравитационных линз, а именно, возникающая бесконечность коэффициента усиления, характерна для всей фокальной полуоси. Подобная бесконечность появляется и в оптических линзах, только наблюдается она всего в одной фокальной точке F = D оптической оси. Рассмотренное бесконечное значение коэффициента усиления по физическим представлениям является следствием приближения геометрической оптики, игнорирующей волновую природу света. Законы геометрической оптики применимы лишь в предельном идеализированном случае, когда длина волны считается бесконечно малой величиной. В этом приближении точечным источникам соответствуют точечные изображения, порождающие бесконечные яркости. В волновой же оптике пучок света, излучаемый даже точечным источником, никогда не даст точечного изображения, его размеры пропорциональны длине волны , т.е. всегда будут конечными, а значит конечным будет усиление излучения. В нашем случае для устранения бесконечных коэффициентов усиления достаточно ввести в рассмотрение источник , имеющий некоторый конечный угловой размер. Световой поток от такого объекта после прохождения линзы будет формировать конечные по своим размерам изображения, как это видно из рис. 5, с конечными значениями коэффициента усиления q. Это оказывается справедливым как для гравитационных, так и для оптических линз. Таким образом, вместо бесконечных коэффициентов усиления мы можем вычислить более отвечающие реальности конечные значения этих величин. На оптической оси они будут принимать некоторые максимальные значения q_max. Впервые эти величины для источников с конечными угловыми размерами были рассчитаны Г. А. Тиховым в 1937 г.

Прежде чем перейти к рассмотрению конкретных примеров наблюдения гравитационно-линзовых систем, обратим внимание на возможность красивого решения с помощью гравитационных линз одной практической задачи релятивистской астрофизики. Речь идет об определении важной космологической величины - постоянной Хаббла Н, характеризующей скорость расширения Метагалактики. Для знакомства с основами современной космологии можно порекомендовать увлекательную книгу И. Д. Новикова "Эволюция Вселенной" (Москва, "Наука", 1990 г.). Более конкретно постоянная Хаббла является коэффициентом пропорциональности между радиальной скоростью "разбегания" отдаленных объектов (галактик, квазаров) и расстоянием до них :

(20)

Из этого простого соотношения видно, что скорость удаления объектов тем больше, чем дальше они расположены от наблюдателя. Важным наблюдательным фактом является отсутствие зависимости постоянной Хаббла от углов наблюдения и местоположения наблюдателя. Иными словами - расширение Метагалактики изотропно и однородно. Современная астрофизика располагает несколькими способами определения постоянной Хаббла, однако единого мнения относительно ее точного значения среди астрофизиков пока нет. Интервал используемых в настоящее время значений величины Н весьма широк - (50-100) км/(сМпс), поэтому более точное ее определение является в настоящее время одной из самых актуальных задач астрофизики. Обратная величина постоянной Хаббла имеет размерность времени (Т - 1/Н) и дает оценку продолжительности расширения Метагалактики с его начала ("Большого взрыва") до сегодняшнего момента. Интервалу значений Н, таким образом, соответствует интервал времени расширения Т приблизительно 10-20 миллиардов лет.

Идея использования гравитационных линз для определения постоянной Хаббла впервые была высказана С. Рефсделом за 15 лет до открытия гравитационно-линзовой системы и дает еще один, очень сильный, метод оценки этой величины. В основе традиционных способов определения постоянной Хаббла так или иначе лежит использование соотношения (20), из которого видно, что для этой цели необходимо знать скорости удаленных объектов и расстояния до них. Первая часть задачи не представляет больших проблем, поскольку лучевые скорости можно установить по измерениям красных смещений внегалактических объектов. При малых скоростях (v/c<<1) эти две величины связаны между собой простым соотношением z = v/c. При больших (релятивистских) скоростях эта формула уже не точна, однако остается функциональная зависимость между красным смещением и скоростью z = z(v). Вторая часть задачи - определение расстояний до объектов - сталкивается уже с немалыми трудностями, причем сделать это становится тем сложнее, чем дальше они расположены. Использование гравитационных линз для определения постоянной Хаббла как раз и позволяет преодолеть эти осложнения. Остановимся на этом более подробно, для чего снова обратимся к рис. 3. Траектории фотонов 1 и 2, огибающие гравитационную линзу с противоположных сторон, будут одинаковой длины (L₁ = L₂) только в одном случае, когда источник расположен на прямой наблюдатель-линза (как и прежде, подразумевается сферическая симметрия гравитационного поля). Следовательно, одновременно излученные фотоны в одно и то же время попадут в телескоп наблюдателя. При смещении источника с оптической оси эти фотоны будут лететь к наблюдателю уже разное время: t₁ = L₁/c и t₂ = L₂/c, так как расстояния, ими проходимые, различны. Разница времени пролета фотонами расстояний L₁ и L₂ называется временем задержки сигнала: dt = dL/C. Измерение величины dt как раз и дает возможность определить постоянную Хаббла. В самом общем виде связь между этими величинами выражается следующим образом:

(21)

В правой части этого равенства символически обозначена функциональная зависимость от наблюдаемых и модельных величин: - угловые расстояния между гравитационной линзой и изображениями, Z - красные смещения линзы и источника, М - масса гравитационной линзы, q- космологический параметр замедления, зависящий от конкретной космологической модели. Может появиться законное сомнение: измеряема ли в принципе сама величина задержки dt; поскольку неясно, на первый взгляд, как маркировать приходящие к наблюдателю световые пучки 1 и 2. Природа помогает нам и здесь, так как большая часть отдаленных линзируемых источников - квазары, а это объекты с переменной интенсивностью излучения. Если взять в качестве начального момента излучения какую-нибудь максимальную фазу блеска квазара, то фиксация наблюдателем этой фазы для лучей 1 и 2 будет происходить в разные моменты времени, разница между которыми равняется величине времени задержки dt. Необходимо учитывать еще одно важное обстоятельство - измеряемая наблюдателем величина dt представляет собой сумму двух разных по своей природе членов: dt = dt₁ + dt₂, один из которых является чисто геометрическим, другой - гравитационного происхождения. Если смысл первого слагаемого уже понятен из рассмотренной геометрии хода лучей, то появление второго обусловлено релятивистским эффектом замедления времени в гравитационном поле. При сравнительно небольших расстояниях до источников оба этих члена близки друг к другу по величине, однако для удаленных объектов геометрический член начинает доминировать. Первые оценки постоянной Хаббла описанным способом были сделаны разными группами исследователей с использованием гравитационно-линзовой системы 0957+561А, В. Западно-европейской группой в результате анализа 8-летних наблюдений за блеском этого переменного квазара было получено значение времени задержки dt порядка 415 суток и соответственно ограничение на величину постоянной Хаббла: Н 85 км/(секъМпс). Этот результат относится к концу 80-х годов. Последние исследования (90-е годы) дают более низкие значения величины Н. В частности, группа астрономов САО (Специальная Астрофизическая Обсерватория на северном Кавказе) по тем же рядам наблюдений квазара 0957+561 получила более высокое значение времени задержки dt порядка 530 суток и соответственно более низкий уровень ограничения постоянной Хаббла: Н < 68 км/(секъМпс). Уже сам факт получения разных числовых результатов по одним и тем же данным говорит о том, что эта задача далеко не так проста, как могло бы показаться на первый взгляд. К подобному разбросу результатов, вообще говоря, приводят различные факторы, оставшиеся за пределами нашего схематического рассмотрения. Это и сохранившийся до настоящего времени некоторый произвол в выборе параметров модели гравитационной линзы, размеры и качество рядов наблюдений (чем дольше и тщательней проводятся наблюдения, тем достоверней результат), и, конечно, сам результат, который даже при всех остальных одинаковых условиях зависит от методики обработки рядов наблюдений. Именно благодаря модифицированному методу обработки наблюдательных данных и была получена астрономами САО новая оценка постоянной Хаббла.

Астрофизики ищут гравитационные линзы

Деформация изображений источников и усиление интенсивности излучения это основные эффекты гравитациоонных линз, наблюдательные проявления которых наиболее доступны для исследований. С другой стороны, вероятность наблюдения этих эффектов должна возрастать с увеличением расстояний до источников, поскольку возрастает возможность появления вблизи световых траекторий больших гравитирующих масс. Это наводит на мысль о целесообразности поиска гравитационных линз среди наиболее удаленных, тесно расположенных источников с угловыми расстояниями между компонентами от долей секунды до нескольких секунд. Такие объекты в природе существуют, это квазары - квазизвездные внегалактические объекты (КЗО), самые мощные излучатели энергии в Метагалактике, многие из которых в десятки и сотни раз превосходят светимость ярких галактик. Сразу же возникает вопрос: каким образом можно отличить "миражи" от физически самостоятельных близких квазаров и возможно ли вообще это сделать? Здравый смысл подсказывает, что если исследуемые объекты порождаются одним источником, то их "портреты" (физические характеристики) должны быть идентичными. Уже это предположение дает возможность сформулировать основные наблюдательные критерии, по которым мы смогли бы узнать линзированные источники. Во-первых, у таких объектов должны быть одинаковыми спектральные характеристики и определяемые по ним красные смещения. Во-вторых, похожими окажутся фотометрические характеристики, причем длительные наблюдения объектов должны установить тождественность характера их переменности, если речь идет о квазарах. Наконец, к важнейшему признаку линзируемости нужно отнести обнаружение самого объекта, создающего изображения источника. Однако, если буквально следовать этому критерию, то можно легко впасть в заблуждение. Например, черную дыру, создающую миражи, наблюдатель может и не обнаружить, и в результате сделает неверный вывод. Более того, и сформулированные выше другие критерии так же не могут дать стопроцентной гарантии в правильности сделанной интерпретации. Выход из этого один - возможно более полное изучение объектов, выходящее за рамки основных критериев и соответствующих им тестов, которые хотя и являются необходимыми этапами исследований, но не всегда достаточными. Именно поэтому исследователь обычно подвергает строгому тестированию каждый заинтересовавший его объект, а значит каждая открытая гравитационная линза неизбежно проходила все основные этапы исследований. Начались же эти открытия, как нам уже известно, с двойного квазара 0957+561А,В.

1. КЗО 0957+561 А,В. Исследования этого объекта проводились в начале 1979 г. с целью отождествления оптических звездообразных источников, близких по блеску (около 17^m) с дискретным радиоисточником. Угловое расстояние между компонентами А и В этого источника соответствует ~ 6", а координаты для А имеют значение: прямое восхождение a_A = 09^h57^m53^s и склонение d_A = 56^o08'23". Нетрудно заметить, что координаты в приближенном виде (с точностью до минут) входят в название объекта, являясь его как бы "визитной карточкой". Неожиданность принесли спектры. У обоих компонентов они оказались тождественными. Затем по эмиссионным линиям спектра СIII 1909 А и СIV 1549 А были измерены красные смещения объектов. Они также оказались практически равными (z_A = z_B =1,40). Эти факты и натолкнули астрономов на мысль, что объекты А и В являются миражами одного источника. Вскоре после возникновения гипотизы о гравитационной линзе была обнаружена сама линза - гигантская эллиптическая галактика, расположенная на прямой между компонентами А и В и на угловом расстоянии = 1" от В. Измерение красного смещения галактики-линзы дало предсказанное значение z = 0,39. Уместно заметить в связи с этим, что красные смещения являются индикаторами космологических расстояний (хотя и довольно грубыми), что видно из формулы z = Hr/c (Н - постоянная Хаббла). Они выражают расстояния, в отличие от метрической системы единиц (см, м) и астрономической системы (световой год, парсек), безразмерным числом. В соответствии с приведенной формулой, чем больше расстояние, тем большее значение имеет величина z. Исследование галактики-линзы показали, что она является самым ярким членом скопления галактик. Это дает основание считать, что свою лепту в создание изображений источника должно вносить и скопление, масса которого приблизительно на два порядка превышает массу галактики-линзы, равную = 10¹² Mc, где Mc - масса Солнца. Некоторые исследователи считают, что модели гравитационно-линзовой системы, наиболее полно воспроизводящие наблюдательные данные, должны учитывать не только эти два важных фактора, предполагающие реальное распределение вещества как в галактике, так и в скоплении. В такую модель должна быть включена и масса скрытого от наблюдателя вещества, входящего в состав скопления. Более того, все реалистичные модели прогнозируют существование третьего изображения источника, расположенного внутри галактики-линзы вблизи ее ядра. Обнаружение этого изображения явилось бы хорошим подтверждением основных принципов моделирования гравитационно-линзовых систем тем более, что в последнее время были получены обнадеживающие данные по наблюдениям в радиодиапазоне. Среди всех известных гравитационных линз объект 0957+561 к настоящему времени изучен наиболее основательно, причем исследования ведутся в очень широком диапазоне длин волн от рентгеновского излучения с искусственных спутников Земли до радиодиапазона. Большое значение астрофизики придают при этом систематическим наблюдениям за блеском пары "близнецов". Мы уже знаем, что увеличение объема таких данных необходимо для более надежного определения времени задержки dt светового сигнала и соответственно для более точной оценки важной космологической величины - постоянной Хаббла.

2. КЗО 1115+080 А,В,С. Открытие первой гравитационно-линзовой системы подхлестнуло поиски других аналогичных объектов. Вскоре усилия астрофизиков дали результат. В процессе исследования тройного квазара 1115+080 А,В,С весной 1980 г. американскими астрономами (группа Веймана) были получены эмиссионные спектры всех трех составляющих, оказавшиеся идентичными. Совпали также и красные смещения этих объектов (z = 1,722), измеренные по наиболее сильным эмиссионным линиям спектра CIV 1549 A и CIII 1909 А. Это и послужило основанием для гипотизы о новом кандидате гравитационной линзы. Обращает на себя внимание более сложная структура объекта 1115+080 по сравнению с системой 0957+561. Кроме большего числа изображений его отличает от первой гравитационно-линзовой системы компактность - все три компонента уместились на небольшой площадке = 2"х2". Такая скученность объектов, да еще при условии значительного превышения потока излучения составляющей А над остальными, затрудняет фотометрический и спектральный анализ двух других (В и С). Сильный источник подавляет более слабые. Так, если яркий компонент А имеет визуальную звездную величину, равную = 15,9^m, то звездные величины других имеют значения: m_в > 19^m, m_с > 18^m, т.е. их световые потоки примерно в 16 и 6 раз слабее, чем у яркого соседа А. В следующем 1981 г. объект А был разрешен на многозеркальном телескопе на две составляющие А₁ и А₂, разнесенные на угловое расстояние = 0,54". Немало усилий пришлось приложить исследователям на поиск самой линзы, создающей наблюдаемые изображения квазара. Долгое время ее никому не удавалось обнаружить, пока не появилось сообщение о том, что это удалось сделать на обсерватории Мауна-Кеа, расположенной на Гавайских островах. Между компонентами А₁ и А₂ был выявлен слабый объект, оказавшийся галактикой. Но это была не единственная галактика в окрестности 1115+080, кроме нее были найдены еще две галактики с красными смещениями: z₁ = 0,304 и z₂ = 0,306. Напрашивается предположение, что все три обнаруженные галактики и создают линзовый эффект. В пользу такой версии, свидетельствует структура системы изображений, вызванная неоднородным характером гравитационного поля линзы. Окончательный ответ, очевидно, будет получен в результате дальнейших исследований - наблюдений и моделирования этой сложной системы. Согласно одной из разработанных моделей ожидаемое число изображений квазара 1115+080 равно даже пяти. Более того, в научной печати уже появилось сообщение об обнаружении пятого миража, но оно нуждается в проверке.

Мы не ставим своей целью рассказать о всех гравитационно-линзовых системах, в этом нет необходимости. Цель другая: дать представление о всех известных типах макролинзирования на некоторых конкретных наиболее интересных примерах, хотя и не всегда достоверно подтвержденных. Именно поэтому дальнейшие примеры гравитационных линз будут следовать без строгого соблюдения хронологического порядка их открытия.

3. КЗО 2237+0305. Начало исследований этого объекта было ознаменовано сюрпризом. В 1984 г. на Уипплской обсерватории (США) проводились наблюдения сравнительно яркой (m = 15^m) и недалеко расположенной (z = 0,039) спиральной галактики 2237+0305. Неожиданностью для наблюдателей стало обнаружение в непосредственной близости от центра галактики (0,3") яркого объекта, иденцифицированного как квазар. Измерения красного смещения показали его значительную удаленность (z = 1,695). Это означало, что два разных по своей природе объекта оказались примерно совмещенными с линией наблюдатель-центр галактики-квазара, так что последний выглядел как бы частью галактики. Отсюда неизбежно следовало, что квазар должен каким-то образом линзироваться галактикой, хотя и не вполне ясен был характер линзирования. Так как было получено лишь одно изображение квазара, можно было бы допустить возможность усиления излучения и некоторое смещение его положения на небесной сфере от истинного. Правда, высказывалась и другая точка зрения на происхождение этого "кентавра". Обосновывалась она с привлечением гипотезы "локальных квазаров", основная идея которой состоит в том, что в районе квазаров с некоторым красным смещением допускается возможность существования туманностей с меньшими красными смещениями. И хотя у близких квазаров (малое z) такие туманности наблюдались, справедливость гипотезы в отношении далекого квазара 2237+0305 требовала каких-то дополнительных наблюдательных подтверждений. Но их не было. Противостояние идей было разрешено наблюдениями объекта 2237+0305 в 1987 г. на 3,6-м телескопе обсерватории Мауна-Кеа, когда квазар был расщеплен на четыре звездообразных, близких по яркости объекта. Систему четырех изображений А, В, С, D характеризует высокая степень дискретной симметрии, что дало повод назвать эту систему "крестом Эйнштейна". Максимальное угловое расстояние между компонентами не превышает ~1,8". Близость полученных изображений друг к другу создает известные препятствия для раздельного изучения каждого из этих объектов, в частности, для получения их спектров. И это долго не удавалось сделать, но в 1989 г. недостающие исследования были проведены. Измерения показали тождественность эмиссионных спектров всех четырех объектов - "космическая криминалистика" сказала свое слово. Основной вклад в создание четырех изображений квазара, по-видимому, вносит галактическое ядро с несиммтричным (квадрупольным) распределением гравитирующей массы, что неплохо описывается соответствующей моделью гравитационно-линзовой системы. Но картина может оказаться сложнее. По наблюдениям объекта в узкой полосе эмиссионной линии CIII 1909 A выявлен "след" возможного пятого изображения. Если этот предварительный результат подтвердится, то и в модель гравитационной линзы придется внести дополнительные коррекции. При моделировании системы 2237+0305 необходимо также учитывать эффект микролинзирования фонового квазара. Речь идет об усилении излучения источника, вызываемого звездами галактики при пересечении их траекторий с лучом наблюдатель-квазар. Вариации блеска изображений источника могут быть весьма значительными и достигать нескольких звездных величин.

4. КЗО 1146+111 В,С. Природа этого объекта неясна до сих пор. Различные точки зрения на его происхождение вполне характеризуют степень нашего "знания", и тем поучительней может оказаться этот пример. Согласно одной гипотезе, два квазара 1146+111 В,С, имеющие примерно одинаковую яркость (m_b = m_c = 19), могут быть миражами одного объекта, разделенными друг от друга необыкновенно большим для гравитационно-линзовой системы расстоянием 157". С другой, "консервативной", точки зрения они являются физически самостоятельными квазарами, имеющими, однако, некоторые общие свойства. Существуют наблюдательные свидетельства как одного, так и другого предположения.

Вскоре после опубликования в 1979 г. сообщения об избыточной концентрации квазаров в небольшой области, центр которой определялся координатами a = 11^h46^m14^s, d = 11^o11'42", были измерены красные смещения девяти квазаров этой области. У двух из них (В и С) красные смещения оказались примерно одинаковыми z = 1,01. Идея гравитационных линз возникла значительно позже, в 1986 г., когда было высказано предположение о том, что столь высокое расщепление изображений могло быть вызвано гравитационным полем космической струны. Последовавшие затем спектральные измерения объектов В и С в диапазоне 4600-7800 А показали тождественность спектров, а уточненные красные смещения по эмиссионной линии MgII 2798 A также оказались одинаковыми z = 1,012. В той же работе была выдвинута гипотеза о том, что линзой может служить гигантская черная дыра с массой M = 10₁₂Mc. Дальнейшие исследования пары 1146+111 В,С охладили головы поклонников гравитационных линз - в инфракрасной и ультрафиолетовой областях характеристики спектров оказались разными. Это привело к тому, что часть исследователей бросилась в другую крайность, отбрасывающую гравитационно-линзовое происхождение пары В и С. Однако указанные наблюдательные аргументы, хотя и очень важные, не устраняют полностью идею линзирования. Достаточно заметить в связи с этим, что время задержки сигнала для двух квазаров составляет величину dt > 1000 лет, что значительно превышает характерный масштаб времени переменности самих квазаров. Следствием этого может быть, в частности, большая разница "загрязнений" спектров, проявляющаяся как раз в ультрафиолетовом и инфракрасном диапазонах. Поэтому для установления истинной природы объекта 1146+111 и ему подобных потребуются, по-видимому, другие, более тонкие исследования и критерии. Во всяком случае, приведенные наблюдательные факты, как и некоторые другие (например, отсутствие заметных флуктуаций микроволнового фонового излучения на гравитационной линзе, свидетельствующее не в пользу линзирования), должны приводить к более жестким ограничениям на модель гравитационной линзы. Одно из таких ограничений приводит, в частности, к необычно низкой относительной концентрации барионной материи в линзе - . Что это - проявление скрытой материи, состоящей из легких частиц, или "след" чего-то такого, чему не придумано даже название? Сказанное относится к одиночной гравитационной линзе той или иной природы. Однако существуют модели, состоящие из нескольких компактных линз, которые также могут производить большое расщепление изображений.

5. КЗО 1548+114 А,В. До сих пор приводились примеры линзирования квазаров галактиками и галактическими скоплениями (кластерами), не считая экзотических случаев черных дыр, космических струн и скрытой материи. Пара квазаров 1548+114 А,В представляет собой, по-видимому, единственный в своем роде случай линзирования одним из членов пары другого. Эти два квазара, открытые Вамплером с сотрудниками в 1973 г., долгое время считались обыкновенной тесной парой разных объектов с угловым расстоянием между ними = 4,8". Красное смещение одного из них 1548+114 А составляет величину z = 0,44, т.е. расположен он от нас сравнительно близко; другой квазар 1548+114 В с красным смещением z = 1,9 - гораздо дальше первого. Такие с очевидностью разные объекты и спектры должны иметь неодинаковые, что и было зафиксировано наблюдателями. Уникальность ситуации состоит в том, что более близкий квазар А в силу своей близости к линии квазар В-наблюдатель должен неизбежно линзировать более отдаленный объект В. Впервые на такую возможность астрофизики обратили внимание только в 1986 г. Однако реальность осложняется наличием трех фоновых галактик, расположенных приблизительно в 10" от квазаров и являющихся составной частью галактического скопления. Этот кластер с тремя галактиками хотя и вносит определенную путаницу в картину линзирования, не устраняет исключительной возможности оценки массы близкого квазара по его гравитационному воздействию на излучение далекого квазара. Грубую оценку массы гравитационной линзы можно сделать уже на основе простейшей линзовой модели, содержащий один-единственный объект А. Но более полная модель, включающая распределение массы в кластере, массу квазара А и массы трех галактик, приводит к более строгому ограничению на массу квазара А: и дает возможность оценить поверхностную плотность массы скопления галактик: o < 0,3 г/см². Следует отметить также и возможность расщепления изображения квазара В на два компонента. Такое раздвоение теоретически зависит от характера распределения плотности вещества квазара А. Это обстоятельство открывает возможности детального изучения структуры квазара-линзы, с трудом поддающегося исследованиям другими методами. Расщепление изображения квазара В, в частности, будет наиболее значительным, если исходить из точечного представления в модели квазара-линзы, тогда второе изображение для В должно находиться в пределах 1" от линзы. Такая близость двойника от яркого объекта несомненно затруднит его поиск, однако вряд ли это остановит астрофизиков.

6. MG 1654+1346 - "кольцо Эйнштейна". Кольцевые изображения источников возникают в тех редких случаях, когда наблюдатель, источник и гравитационная линза расположены строго на одной линии. Здравый смысл подсказывает, что вероятность подобных событий невелика и должна прямо зависеть от размеров источников излучения: она будет тем меньше, чем меньшие угловые размеры имеют эти источники. Отсюда следует, что для наблюдателя практическую ценность могут представлять протяженные излучающие структуры. Но как раз такие структуры характерны для радиоисточников, причем в гораздо большей степени, чем для излучателей в оптическом диапазоне. Значит, если пытаться искать кольца, то делать это скорее всего нужно с помощью радиотелескопов. Нынешняя фаза исследований гравитационно-линзовых систем подтверждает пока эти соображения.

Радиоисточник MG 1131+0454 стал первым удаленным излучающим объектом, кольцевое изображение которого было получено в 1987 г. с помощью радиоинтерферометра VLA (Very Large Array - Очень Большая Решетка). Возможно, это событие так и осталось бы счастливым курьезом для наблюдателей, если бы в следующем 1988 г. на той же системе VLA не была получена еще одна кольцевая структура объекта MG 1654+1346 на частотах 1,5 ГГц и 5 ГГц. Наблюдениями была выявлена следующая картина радиоизображения источника: кроме самого кольца с двумя максимумами (А, В) на противоположных его сторонах с расстоянием 2,13", между ними был обнаружен более слабый компонент С на расстоянии 6,8" от центра кольца на линии, соединяющей два пика интенсивности. Несколько позже в том же году уже в оптической области было обнаружено еще два объекта - красная галактика С, расположенная точно в центре кольца, и голубой звездный объект Q, локализованный примерно посередине между центром кольца и радиокомпонентом С. Звездный объект по характеру спектра был идентифицирован как квазар, имеющий красное смещение z_Q = 1,74. Красная галактика расположена значительно ближе к наблюдателю, величина ее красного смещения, определенная по спектру, оказалась равной z_Q = 0,254. Все эти объекты, видимо, имеют непосредственное отношение к гравитационно-линзовой системе, и их перечисление понадобилось для того, чтобы показать, насколько реальная ситуация может быть сложней простых схем, рассмотренных нами раньше. Вся полученная информация дает возможность представить себе картину происходящего в целом. Оптический квазар-источник A, по-видимому, имеет два протяженных радиолепестка с максимальными значениями интенсивности, локализованными l'4" по обе его стороны. Галактика-линза G создает два радиоизображения источника (кольцо и компонент С) и одно оптическое, несколько усиленное и смещенное от истинного положения. Модельная интерпретация этой системы дала возможность рассчитать многие ее параметры, важнейшим из которых является масса галактики-линзы G:Mc. Некоторые исследователи считают, что эффект линзирования создает не одна галактика G. Основанием для такого мнения послужило неадекватное воспроизведение наблюдаемой картины существующими моделями.

Малочисленное семейство кольцевых изображений в 1990 г. пополнилось еще одним, третьим, кандидатом. У наблюдавшегося до этого времени двойного радиоисточника, по-видимому, линзированного, при повторных радионаблюдениях была выявлена симметричная кольцевая структура. Для подтверждения этого результата и установления подлинного статуса этого объекта, конечно, потребуются дополнительные усилия астрофизиков, что, впрочем, относится и к двум другим, открытым раньше кольцам.

7. Светящаяся дуга в скоплении Abell 370. Самые первые сведения о гигантских светящихся межгалактических дугах были получены американскими астрономами в 1976 г. в процессе реализации программы по изучению галактических скоплений. В следующее десятилетие происходило накопление данных об этих объектах и предпринимались попытки их как-то объяснить. Согласно гипотезе "светового эха", дуги возникли в результате рассеяния в межгалактической среде всплеска излучения квазара. По другому предположению дуги ассоциировались с ударной волной, вызванной сверхмощным взрывом какого-то объекта в скоплении, а свечение дуги создают молодые звезды, рождение которых вызвано фронтом ударной волны. Но, пожалуй, самое естественное объяснение феномена светящихся дуг связано с идеей гравитационного линзирования, высказанной Б. Пашинским в 1987 г. Изящество этой идеи вместе с ее относительной простотой и привлекли к ней внимание астрофизиков. Всесторонние исследования этих необычных объектов в значительной степени укрепляли позиции идеи линзирования.

С гравитационно-линзовой точки зрения по структуре и происхождению дугообразные миражи занимают как бы промежуточное положение между кратными объектами и кольцами. Это хорошо иллюстрирует рис. 5 с радиально-симметричной гравитационной линзой. По мере того, как источник с конечными угловыми размерами смещается с оптической оси, где он отображается линзой в кольцо, его изображение сначало превращается в два серпа, затем эти серпы все больше стягиваются, и при достаточном удалении от оптической оси становятся практически копиями оригинала по форме. В более реальных случаях даже небольших отклонений от радиальной симметрии такой механизм образования дуг уже непригоден и для объяснения их возникновения приходится применять более сложные процедуры. Необычайно большие угловые размеры светящихся дуг (> 20") свидетельствуют об огромных массах линз, создающих миражи. Именно такие массы характерны для скопления галактик, где эти дуги и наблюдаются. Гигантские же размеры кластеров (десятки угловых минут) делают вероятность покрытия ими источников ощутимой конечной величиной, что и приводит к сравнительно высокой наблюдаемой частоте этого явления.

К настоящему моменту в разных галактических скоплениях открыто около десятка светящихся дуг: Abell 370, Cl 2244-02, Abell 2218, Abell 963, Cl 0024+16 и др. Первые два из этих объектов открыты раньше других и исследованы более полно, поэтому и рассмотрим более подробно один из них - дугу в скоплении Abell 370. На фотопластинках эта дуга имеет вид яркого сегмента окружности (1/6 ее часть), напоминающего елочную гирлянду с лампочками-галактиками. В центре кривизны дуги расположена яркая эллиптическая галактика. С противоположной стороны от центра кривизны в районе другой гигантской эллиптической галактики наблюдается еще одна короткая и слабая дужка. Поражают воображение размеры главной дуги: ее угловая длина равна 21", что соответствует 143 кпс, если принять, что она расположена на том же расстоянии, что и кластер (Z = 0,373). Ширина дуги незначительна - 1,36". На восточном ее конце заметен небольшой разрыв с последующим утолщением. Весь комплекс дуги в пределах круга радиуса (радиуса кривизны 15,1") состоит, таким образом, из двух основных компонентов: диффузной составляющей, содержащей две дуги, одна из которых имеет огромную протяженность, и галактической составляющей, в которую входят галактики скопления. Населенность второй компоненты из-за близости дуги к центру кластера весьма значительна и обнаруживает рост плотности галактик в направлении центра скопления. Принципиальными экспериментами, подтверждающими идею линзирования, должны были бы стать спектральные исследования дуги. При этом красные смещения самой дуги должны значительно превышать величину z для членов скопления. Если спектры и красные смещения для ярких галактик скопления измерить не составляло большой проблемы, и они были измерены с хорошей точностью (z = 0,373), то определение красного смещения разреженной диффузной составляющей (дуги) представляло немалые трудности. После ряда неудачных попыток две группы исследователей сообщили о положительном решении этой задачи. В обоих случаях была надежно идентифицирована эмиссионная линия OII 2727 A, по которой было определено красное смещение дуги: z = 0,725, т.е. источник излучения находится почти вдвое дальше скопления. Другим сильным подтверждением идеи линзирования явилось восстановление основных элементов комплекса дуг Аbell 370 в результате численного анализа модели это - сложной гравитационно-линзовой системы. В качестве линзируемого источника в такой модели была взята спиральная галактика, что вполне соответствовало характеру спектра дуги. Сама гравитационная линза была представлена довольно сложным распределением вещества - на однородном фоне плотности массы основной части скопления () рассматривалось около десятка галактик, создающих линзирующий эффект, две самых крупных из которых имеют массы . В пользу гипотезы линзирования свидетельствуют также фотометрические данные составляющих комплекса дуг Аbell 370. Однако окончательный выбор механизма образования светящихся дуг в этом скоплении будет сделан в будущем, для чего потребуются новые, кропотливые исследования, в частности, поляризационные. Впрочем, возможность такого выбора, если она существует в науке вообще, всегда сопряжена с дополнительными усилиями исследователей.

POST SCRIPTUM

Космические ускорители заряженных частиц, космические мазеры, природные ядерные реакторы,... и вот теперь "космические телескопы". Природа создает не просто материальные объекты исследований, но и сложные "устройства", которые сами могут служить инструментами исследований. Она не устает снабжать нас всевозможными идеями не только в области науки, но и техники, технологии, в гуманитарных сферах (литература, искусство, философия, право...). Все это, казалось бы, свидетельствует о некоторой органической связи Природы и Человека. Что касается происхождения Человека и его места в мире, то так оно, видимо, и есть, однако своей деятельностью он все время пытается оспаривать эти родственные связи. Чего стоит, например, его так называемые "познание" и "освоение" Природы, грозящие его собственному существованию. Вряд ли это нужно приписывать мести Природы за нанесенный ей ущерб. Природа мудра, и эти планы уничтожения скорее всего не входят в ее замысел - наверное, ей рано избавляться от недавно появившегося на свет "мыслящего эмбриона" ("мыслящего тростника", по выражению Паскаля). Дело, видимо, в другом, а именно в чрезмерном самомнении эмбриона, проявляющемся в безудержной агрессии против внешнего мира, а, следовательно, и против самого себя. Как, например, он распоряжается отпущенным ему разумом и идеями? Бездумным, бесконечным наращиванием своих усилий по освоению Природы - созданием разрушительной индустрии, все более сложных, чудовищных по мощности машин и оружия, опустошением недр и земной поверхности, химизацией всей жизни и т.д. и т.п. Такой процесс не может иметь никакого положительного смысла, даже если он и называется "прогрессом". Деятельность человека скорее напоминает детскую игру в кубики. Беспорядочное нагромождение кубиков одного на другой рано или поздно кончается саморазрушением выстроенной конструкции. Если уничтожить весь мир эмбрион, даже "глубоко мыслящий", пожалуй, не в состоянии, то разрушить свой дом он может уже сегодня, на это если не "разума", то "умения" у него вполне хватит!

Но коль скоро сегодняшний "прогресс" чреват такими последствиями, то может быть нам попробовать пожить по чисто природным принципам и законам? Может быть, природа, подкидывая нам свои идеи и конструкции, предлагает использовать их в чистом виде без какого бы то ни было привлечения "плодов цивилизации"? Здравый смысл подсказывает, что и эта возможность осуществима, вероятно, лишь в сладких снах и грезах фантастов. Ведь для того, чтобы открыть и использовать те же "космические телескопы", понадобились "плоды цивилизации" - созданные трудом человека инструменты. Существуют ли какие-нибудь другие, не столь опасные для нас, реальные возможности?

Остается, пожалуй, одна-единственная, спасительная для нас возможность - сотрудничество. С кем? Конечно, с ее величеством Природой, другого партнера у нас пока нет. Как невозможно обычное сотрудничество среди людей без доброжелательства и взаимопонимания, так и здесь эти два прекрасных человеческих качества можно взять за основу, переформулировав их в виде двух принципов. Один из них можно было бы определить как принцип минимизации вреда, или ущерба, который может быть нанесен объекту познания (освоения) в окружающем мире, а, значит, и самому субъекту познания - человеку. Это имеет некоторую аналогию со старым принципом "бритвы Оккама", только в оригинальной трактовке бритва обрезает все, что не проверяется опытом и не сводится к интуиции, а в нашем случае отметается все, что наносит Природе существенный ущерб. Другой принцип можно было бы сформулировать как разумное разделение сфер деятельности - Природа берет на себя свою часть деятельности, человек - свою. В качестве иллюстрации можно сослаться на современное состояние исследований в области микромира. Если для проверки теории электрослабых взаимодействий и открытия W_± и Z₀ бозонов оказались достаточными энергии 100 Гэв, что доступно современной ускорительной технике, то для проверки моделей великого объединения, включающих электромагнитное, слабое и сильное взаимодействия в одну схему, понадобится энергия 10¹⁴ Гэв и выше. Ни о каких созданных человеком монстрах-ускорителях, рассчитанных на такие энергии, в обозримом будущем не может идти и речи. И дай нам Бог разума воздержаться от подобных проектов на Земле. Не проще ли поискать источники таких энергий где-нибудь в Космосе? Другой пример. Теория предсказывает существование в Космосе реликтовых доменных структур, отделенных друг от друга так называемыми "стенками" (поверхностями), и космических струн с колоссальными плотностями (более 10¹⁹ г/см). Моделирование таких состояний вещества в земных лабораторных условиях ничего, кроме крупных неприятностей, исследователям (и не только им) не сулит. Но вот астрофизики обнаружили четыре пары двойных галактик в поле объекта Н 0414+00, обладающих попарно сходными свойствами. Именно такие пары источников должны наблюдаться при гравитационном линзировании фоновых объектов космическими струнами. Если дальнейшие наблюдения подтвердят эту гипотезу, то появится прекрасная возможность исследовать такие реликтовые структуры как космические струны и получать экспериментальные ограничения на модели великого объединения.

Природа непрерывно искушает человека, вернее, он искушается ею, решаясь порою на безрассудные мероприятия. Может быть, этого и не следует делать, а вместо того, чтобы рыть землю, достаточно взглянуть на небо, или вместо того, чтобы бессмысленно задирать голову вверх, - всего лишь посмотреть себе под ноги. Не это ли имел ввиду Ф. Тютчев, сказав:

"Природа - сфинкс. И тем она верней

Своим искусом губит человека,

Что, может статься, никакой от века

Загадки нет и не было у ней".

Дорога к Истине далеко не прямолинейна и не единственна. Так религиозный путь - это путь Откровения и Веры; философский путь, онтологический по своей сути - познание бытия как такового; научное же познание базируется на опыте. Среди прочих дорог человек выбрал последнюю, может быть, самую опасную для него, приводящую уже сегодня к столь разрушительным результатам. И вряд ли он уйдет с этой дороги, хотя ему и пришлось бы набить на ней множество шишек и синяков. Но возможно ли познание на основе сформулированных здесь принципов, ведь на первый взгляд они противоречивы? Смущаться не стоит: противоречия - результат неполного знания, на более высоком уровне познания они снимутся. "Лучшее лекарство против половинного знания есть наибольшее знание", - писал А. Пуанкаре. Только такое "наибольшее знание" и должно, видимо, стать целью научного познания существа вида Homo Sapiens. Без этого, скорее всего не будет возможной ни одна из выбранных им дорог: безрассудная детская игра в кубики уже в не очень отдаленном будущем может привести к полному его вырождению.