§ 22. Уравнение времени

Разность между средним временем и истинным солнечным временем в один и тот же момент называется уравнением времени h. На основании (1.18), (1.19) и (1.15) уравнение времени 

h = Tm — T¤ = tm — t¤ = a ¤ — a m.

(1.20)

Из последнего соотношения следует:

Tm = T¤ + h ,

(1.21)

т.е. среднее солнечное время в любой момент равно истинному солнечному времени плюс уравнение времени.

Таким образом, измерив непосредственно часовой угол Солнца t_¤, определяют по (1.18) истинное солнечное время и, зная уравнение времени h в этот момент, находят по (1.21) среднее солнечное время: T_m = t_¤ + 12^h + h.

Так как среднее экваториальное солнце проходит через меридиан то раньше, то позже истинного Солнца, разность их часовых углов (уравнение времени) может быть как положительной, так и отрицательной величиной.

Уравнение времени и его изменение в течение года представлено на рис. 14 сплошной кривой. Эта кривая является суммой двух синусоид — с годичным и полугодичным периодами.

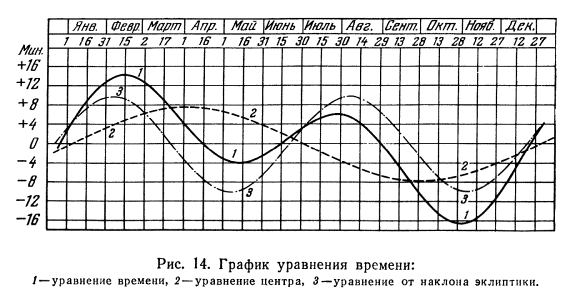
Синусоида с годичным периодом (штриховая кривая) дает разность между истинным и средним временем, обусловленную неравномерным движением Солнца по эклиптике. Эта часть уравнения времени называется уравнением центра или уравнением от эксцентриситета. Синусоида с полугодичным периодом (штрих-пунктирная кривая) представляет разность времен, вызванную наклоном эклиптики к небесному экватору, и называется уравнением от наклона эклиптики.

Уравнение времени обращается в нуль около 15 апреля, 14 июня, 1 сентября и 24 декабря и четыре раза в году принимает экстремальные значения; из них наиболее значительные около 11 февраля (h = +14^m) и 2 ноября (h = —16^m).

Уравнение времени можно вычислить для любого момента. Оно обычно публикуется в астрономических календарях и ежегодниках для каждой средней полуночи на меридиане Гринвича. Но следует иметь в виду, что в некоторых из них уравнение времени дается в смысле «истинное время минус среднее» (h = T_¤ — Т_т) и поэтому имеет противоположный знак. Смысл уравнения времени всегда разъясняется в объяснении к календарям (ежегодникам).