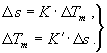§ 23. Связь среднего солнечного времени со звездным

Из многолетних наблюдений установлено, что в тропическом году содержится 365,2422 средних солнечных суток. Нетрудно показать, что звездных суток в тропическом году на единицу больше, т.е. 366,2422.

Действительно, предположим, что в момент весеннего равноденствия некоторого года среднее экваториальное солнце и точка весеннего равноденствия находятся в верхней кульминации. Спустя одни звездные сутки точка весеннего равноденствия снова придет на небесный меридиан, а среднее экваториальное солнце не дойдет до него, так как за звездные сутки оно сместится по небесному экватору к востоку на дугу примерно в 1°. Оно пройдет небесный меридиан после поворота небесной сферы на этот угол, на что потребуется около 4^m времени, а точнее З^m56^s. Следовательно, средние сутки продолжительнее звездных суток на З^m56^s.

Отходя каждые звездные сутки к востоку на дугу в 3^m56^s (или ~1°), среднее экваториальное солнце на протяжении тропического года обойдет весь небесный экватор (подобно одному видимому обороту Солнца по эклиптике) и в момент следующего весеннего равноденствия снова придет в точку весеннего равноденствия. Но в этот момент часовой угол среднего солнца и точки весеннего равноденствия будут отличаться от нуля, так как тропический год не содержит целого числа ни звездных, ни средних суток.

Нетрудно видеть, что, какова бы ни была продолжительность тропического года, число суточных оборотов Солнца за этот промежуток времени будет на единицу меньше, чем число суточных оборотов точки весеннего равноденствия.

Иными словами,

365,2422 средн. солн. суток = 366,2422 звездн. суток,

откуда

и

Коэффициент

(1.22)

служит для перевода промежутков среднего солнечного времени в промежутки звездного времени, а коэффициент

(1.23)

— для перевода промежутков звездного времени в промежутки среднего солнечного времени. Таким образом, если промежуток времени в средних солнечных единицах есть DT_m, а в звездных единицах Ds, то

(1.24)

Oтсюда, в частности, следует, что

24^h	средн. солн. вр.	=	24^h03^m56^s,555	звездн. вр.
1^h	» » »	=	1  00  09 ,856	» »
1^m	» » »	=	01  00 ,164	» »
1^s	» » »	=	01 ,003	» »
24^h	звездн. времени	=	23^h 56^m 04^s,091	средн. солн. вр.
1^h	» »	=	59   50 ,170	» » »
1^m	» »	=	59 ,836	» » »
1^s	» »	=	0 ,997	» » »

Для облегчения вычислений на основании соотношений (1.24) составляются подробные таблицы, по которым любой промежуток времени, выраженный в одних единицах, легко можно выразить в других единицах.

Для приближенных расчетов можно считать, что звездные сутки короче средних (или, наоборот, средние длиннее звездных) приблизительно на 4^m, а один звездный час короче среднего (или средний длиннее звездного) — на 10^s. Например, 5^h среднего времени » 5^h00^m50^s звездного времени, а 19^h звездного времени »18^h56^m50^s среднего времени.

Пусть звездное время в некоторый момент на данном меридиане равно s, а звездное время в ближайшую предшествующую среднюю полночь на этом же меридиане было S. Значит, после полуночи прошло (s — S) часов, минут и секунд звездного времени. Этот промежуток, если его выразить в единицах среднего солнечного времени, равен (s — S) К ' часам, минутам и секундам среднего времени. А так как в среднюю полночь среднее солнечное время равно 0^h, то, следовательно, в момент s по звездному времени среднее солнечное время будет Т_т = (s — S) К'.

Наоборот, пусть среднее время в некоторый момент на данном меридиане равно Т_т. Это значит, что после средней полуночи прошло Т_т часов, минут и секунд среднего времени. Этот промежуток времени равен Т_mК звездных часов, минут и секунд, которые прошли от средней полуночи. И если в среднюю цолночь определенной даты на данном меридиане звездное время было S, то в момент Т_т звездное время будет s = S + Т_m К.

Таким образом, в обоих случаях нужно знать звездное время S в среднюю полночь на данном меридиане.

В астрономических ежегодниках дается звездное время S₀ для каждой средней полуночи на меридиане Гринвича. Зная S₀, легко вычислить S на любом другом меридиане, если известна его долгота от Гринвича l , выраженная в часах и долях часа.

Действительно, так как средние сутки длиннее звездных на З ^m б ^s,ббб, то S₀, так же как и S, ежесуточно увеличивается на З ^m 56 ^s, 555. Следовательно, на меридиане с долготой l к востоку от Гринвича звездное время в среднюю полночь будет меньше на величину так как средняя полночь на этом меридиане наступит раньше гринвичской полуночи на l ^h. Отсюда

(1.25)

(Долгота l  отсчитывается положительной к востоку от Гринвича.) Для приближенных расчетов, с точностью до 5 минут, звездное время S в среднюю полночь на любом меридиане можно вычислить по следующей таблице:

Дата		s	Дата		s	Дата		s
Сентябрь	22	0^h	Январь	21	8^h	Май	23	16^h
Октябрь	22	2	Февраль	21	10	Июнь	22	18
Ноябрь	22	4	Март	23	12	Июль	23	20
Декабрь	22	6	Апрель	22	14	Август	22	22

При этом нужно иметь в виду, что за каждые сутки звездное время уходит вперед относительно среднего времени приблизительно на 4^m.