§ 28. Сферический треугольник и основные формулы сферической тригонометрии

Многие задачи астрономии, связанные с видимыми положениями и движениями небесных тел, сводятся к решению сферических треугольников.

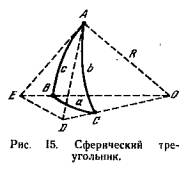
Сферическим треугольником называется фигура АВС на поверхности сферы, образованная дугами трех больших кругов (рис. 15).

Углами сферического треугольника называются двугранные углы между плоскостями больших кругов, образующих стороны сферического треугольника. Эти углы измеряются плоскими углами при вершинах треугольника между касательными к его сторонам.

Обычно рассматриваются треугольники, углы и стороны которых меньше 180°. Для таких сферических треугольников сумма углов всегда больше 180°, но меньше 540°, а сумма сторон всегда меньше 360°. Разность между суммой трех углов сферического треугольника и 180° называется сферическим избытком s , т.е.

s = ÐA + ÐB + ÐC — 180°.

Площадь сферического треугольника s равна

,

где R — радиус сферы, на поверхности которой образован треугольник.

Сферический треугольник, таким образом, отличается по своим свойствам от плоского, и применять к нему формулы тригонометрии на плоскости нельзя.

Возьмем сферический треугольник АВС (рис. 15), образованный на сфере радиуса R и с центром в точке О.

Из вершины А проведем касательные AD и АЕ к сторонам b и с до пересечения их с продолжениями радиусов ОС и 0В, лежащих в одной плоскости с соответствующей касательной. Соединив прямой точки пересечения D и Е, получим два плоских косоугольных треугольника ADE и ODE с общей стороной DE. Применяя к этим треугольникам теоремы элементарной геометрии, напишем:

DE² = OD² + ОЕ² — 2OD× ОЕ × cos a,

DE² = AD² + АЕ² — 2AD× АЕ× cos A.

Вычитанием второго равенства из первого получим:

2OD × ОЕ× cos a = OD^2 — AD^2 + ОЕ^2 — АЕ^2 + 2AD × АЕ × cos A.

(1.31)

Из прямоугольных плоских треугольников ОАЕ и ОАD следует:

OD² — AD² = R²; OE² — AE² = R²;

AD = R tg b ; АЕ = R tg с ;

Подставив эти соотношения в формулу (1.31) и произведя соответствующие сокращения и переносы, получим

cos а = cos b cos с + sin b sin с cos A ,

(1.32)

т.е. косинус стороны сферического треугольника равен произведению косинусов двух других его сторон плюс произведение синусов тех же сторон на косинус угла между ними.

Формулу (1.32) можно написать для любой стороны треугольника. Напишем ее, например, для стороны b:

cos b = cos с cos a + sin с sin a cos B

и, подставив в нее cos сх из формулы (1.32), получим

cos b = cos с (cos b cos с + sin b sin с cos A) + sin с sin a cos B.

Раскрыв скобки и перенеся первый член правой части в левую, будем иметь:

cos b (l — cos² с) = sin b sin с cos с cos A + sin c sin a cos B.

Заменив (1 — cos² с) на sin² с и сократив все на sin c, окончательно получим

sin a cos В = sinc cos b — cos c sin b cos A,

(1.33)

т.е. произведение синуса стороны на косинус прилежащего угла равняется произведению синуса другой стороны, ограничивающей прилежащий угол, на косинус третьей стороны минус произведение косинуса стороны, ограничивающей прилежащий угол, на синус третьей стороны и на косинус угла, противолежащего первой стороне.

Формула (1.33) называется формулой пяти элементов. Ее можно написать по аналогии и для произведений sin a cos С, sin b cos A, sin b cos С, sin с cos A и sin с cos В.

Решим теперь равенство (1.32) относительно cos A :

Возведя обе части последнего равенства в квадрат и вычтя их из 1, получим:

или

Раскрыв скобки и разделив обе части этого выражения на sin² а, получим

Полученное выражение совершенно симметрично относительно a, b и с, и заменяя A на В, а на b или A на С и а на с, напишем

откуда

		(1.34)
или

т.е. синусы сторон сферического треугольника пропорциональны синусам противолежащих им углов; или отношение синуса стороны сферического треугольника к синусу противолежащего угла есть величина постоянная.

Три выведенных соотношения (1.32), (1.33), (1.34) между сторонами и углами сферического треугольника являются основными; из них можно получить много других формул сферической тригонометрии. Мы ограничимся выводом одной только формулы для прямоугольного сферического треугольника. Положим А = 90°; тогда sin А = 1, cos A = 0, и из формулы (1.33) получим

sin a cos В = sin с cos b.

Разделив обе части этого равенства на sin b и заменив на на , согласно (1.34), будем иметь:

ctg B = sin c ctg b

или

(1.35)

т.е. отношение тангенса одного катета прямоугольного сферического треугольника к тангенсу противолежащего угла равно синусу другого катета.