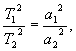§ 40. Законы Кеплера

Кеплер был сторонником учения Коперника и поставил перед собой задачу усовершенствовать его систему по наблюдениям Марса, которые на протяжении двадцати лет производил датский астроном Тихо Браге (1546-1601) и в течение нескольких лет — сам Кеплер.

Вначале Кеплер разделял традиционное убеждение, что небесные тела могут двигаться только по кругам, и поэтому он потратил много времени на то, чтобы подобрать для Марса круговую орбиту.

После многолетних и очень трудоемких вычислений, отказавшись от общего заблуждения о кругообразности движений, Кеплер открыл три закона планетных движений, которые в настоящее время формулируются следующим образом:

1. Все планеты движутся по эллипсам, в одном из фокусов которых (общем для всех планет) находится Солнце.

2. Радиус-вектор планеты в равные промежутки времени описывает равновеликие площади.

3. Квадраты сидерических периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит.

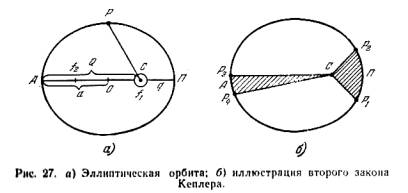
Как известно, у эллипса сумма расстояний от какой-либо его точки до двух неподвижных точек f₁ и f₂, лежащих на его оси АП и называемых фокусами, есть величина постоянная, равная большой оси АП (рис. 27). Расстояние ПО (или ОA), где О — центр эллипса, называется большой полуосью а, а отношение — эксцентриситетом эллипса. Последний характеризует отклонение эллипса от окружности, у которой е = 0.

Орбиты планет мало отличаются от окружностей, т.е. их эксцентриситеты невелики. Наименьший эксцентриситет имеет орбита Венеры (е = 0,007), наибольший — орбита Плутона (е = 0,247). Эксцентриситет земной орбиты е = 0,017.

Согласно первому закону Кеплера Солнце находится в одном из фокусов эллиптической орбиты планеты. Пусть на рис. 27, а это будет фокус f₁ (С — Солнце). Тогда наиболее близкая к Солнцу точка орбиты П называется перигелием, а наиболее удаленная от Солнца точка A — афелием. Большая ось орбиты АП называется линией апсид, а линия f₂P, соединяющая Солнце и планету Р на ее орбите, — радиусом-вектором планеты.

Расстояние планеты от Солнца в перигелии

q = а (1 — е),

(2.3)

в афелии

Q = a (l + e).

(2.4)

За среднее расстояние планеты от Солнца принимается большая полуось орбиты

Согласно второму закону Кеплера площадь СР₁Р₂ , описанная радиусом-вектором планеты за время Dt вблизи перигелия, равна площади СР₃Р₄ , описанной им за то же время Dt вблизи афелия (рис. 27, б). Так как дуга Р₁Р₂ больше дуги Р₃Р₄ , то, следовательно, планета вблизи перигелия имеет скорость большую, чем вблизи афелия. Иными словами, ее движение вокруг Солнца неравномерно.

Скорость движения планеты в перигелии

(2.5)

в афелии

(2.6)

где v_c — средняя или круговая скорость планеты при r = а. Круговая скорость Земли равна 29,78 км/сек » 29,8 км/сек.

Первый и второй законы Кеплера показывают, что третье и четвертое утверждения Коперника (см. § 36) неверны. Третий закон Кеплера записывается так:

(2.7)

где Т₁ и T₂ — сидерические периоды обращений планет, а₁ и a₂ — большие полуоси их орбит.

Если большие полуоси орбит планет выражать в единицах среднего расстояния Земли от Солнца (в астрономических единицах), а периоды обращений планет — в годах, то для Земли а =1 и Т = 1 и период обращения вокруг Солнца любой планеты

(2.8)

Третий закон Кеплера устанавливает зависимость между расстояниями планет от Солнца и периодами их обращения.