§ 51. Третий (уточненный) закон Кеплера

При круговом движении ускорение w = w²r, где угловая скорость , а Т — период обращения по окружности. Следовательно, ускорение

Если рассматривать относительное движение по кругу небесного тела с массой т вокруг центрального тела с массой M, то согласно уравнению (2.17) относительное ускорение

Так как w и w_от — одно и то же ускорение, то, приравняв их правые части, получим

(2.23)

Если рассматривать движение небесного тела по эллипсу, то получится соотношение, аналогичное (2.23), только в нем радиус круга r заменится на большую полуось а, а T будет означать период обращения тела по эллипсу. Напишем это соотношение для двух тел, массы которых т₁ и т₂ , большие полуоси их эллиптических орбит а₁ и a₂ , а периоды их обращений вокруг их центральных тел с массами М₁ и М₂ обозначим через T₁ и T₂ . Тогда

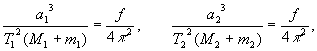
откуда

(2.24)

Это точное выражение третьего закона Кеплера. Если рассматривать движение двух планет вокруг Солнца, т.e. вокруг одного и того же тела (М₁ = М₂ ), и пренебречь массами планет (т₁ » m₂ = 0) в сравнении с массой Солнца, то получим формулу (2.7), выведенную Кеплером из наблюдений:

Так как массы планет в сравнении с массой Солнца незначительны, то формула Кеплера достаточно хорошо согласуется с наблюдениями.

Формулы (2.23) и (2.24) играют большую роль в астрономии: они дают возможность определять массы небесных тел (см. § 58).