§ 63. Определение расстояний до небесных тел

Определение расстояний до тел Солнечной системы основано на измерении их горизонтальных параллаксов, рассмотренных в § 31.

Зная горизонтальный экваториальный параллакс р₀ светила, легко определить его расстояние от центра Земли (см. рис. 20). Действительно, если ТО = R₀ есть экваториальный радиус Земли, ТМ = D — расстояние от центра Земли до светила М, а угол р — горизонтальный экваториальный параллакс светила р₀ , то из прямоугольного треугольника ТОМ имеем

(3.1)

Для всех светил, кроме Луны, параллаксы очень малы. Поэтому формулу (3.1) можно написать иначе, положив

а именно,

(3.2)

Расстояние D получается в тех же единицах, в которых выражен радиус Земли R₀. По формуле (3.2) определяются расстояния до тел Солнечной системы. Быстрое развитие радиотехники дало астрономам возможность определять расстояния до тел Солнечной системы радиолокационными методами. В 1946 г. была произведена радиолокация Луны, а в 1957-1963 гг.— радиолокация Солнца, Меркурия, Венеры, Марса и Юпитера. По скорости распространения радиоволн с = 3 × 10⁵ км/сек и по промежутку времени t (сек) прохождения радиосигнала с Земли до небесного тела и обратно легко вычислить расстояние до небесного тела

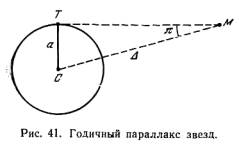
Расстояния до звезд определяются по их годичному параллактическому смещению, которое обусловлено перемещением наблюдателя (вместе с Землей) по земной орбите (рис. 41).

Угол, под которым со звезды был бы виден средний радиус земной орбиты при условии, что направление на звезду перпендикулярно к радиусу, называется годичным параллаксом звезды p. Если СТ = а есть средний радиус земной орбиты, МС = D — расстояние звезды М от Солнца С, а угол p — годичный параллакс звезды, то из прямоугольного треугольника СТМ имеем

(3.3)

Годичные параллаксы звезд меньше 1", и поэтому

(3.4)

Расстояние D по этим формулам получается в тех же единицах, в которых выражено среднее расстояние а Земли от Солнца.