§ 82. Условия наступления солнечных и лунных затмений

Если бы плоскость лунной орбиты совпадала с плоскостью эклиптики, то солнечные и лунные затмения происходили бы каждый синодический месяц. Но плоскость лунной орбиты наклонена к плоскости эклиптики под углом в 5° 09', поэтому Луна во время новолуния или полнолуния может находиться далеко от плоскости эклиптики, и тогда ее диск пройдет выше или ниже диска Солнца или конуса тени Земли, и никакого затмения не случится.

Чтобы произошло солнечное или лунное затмение, необходимо, чтобы Луна во время новолуния или полнолуния находилась вблизи узла своей орбиты, т.е. недалеко от эклиптики.

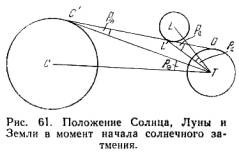
Пусть на рис. 61 С, Т и L обозначают центры Солнца, Земли и Луны и находятся в одной плоскости, перпендикулярной к плоскости эклиптики. Тогда Ð LTC = b есть геоцентрическая эклиптическая широта Луны, и если этот угол будет меньше изображенного на рисунке, то произойдет, хотя и непродолжительное, частное затмение Солнца для точки О на Земле. Угол b равен сумме трех углов, а именно:

b = Ð LTL' + Ð L'TC' + Ð C'TC.

Но угол LTL’ = r₍ есть угловой радиус Луны; L’TC’ = r_¤ — угловой радиус Солнца; угол L'TC' = Ð TL’O — Ð TC'O, где Ð TL'O = р₍ есть горизонтальный параллакс Луны, a ÐTC'O = p_¤ — горизонтальный параллакс Солнца. Следовательно,

b = r₍ + r_¤ + p₍ — p_¤.

Если для величин в правой части принять их средние значения r₍ = 15',5, r_¤ = 16',3, p₍ = 57',0, p_¤ » 8",8, то b = 88',7.

Следовательно, для наступления хотя бы непродолжительного частного затмения Солнца необходимо, чтобы геоцентрическая эклиптическая широта Луны была меньше 88',7. Угловое расстояние центра Луны от узла, т.е. долгота Луны относительно узла Dl может быть вычислена из сферического прямоугольного треугольника < E L. (рис. 62) по формуле

При b = 88',7 и i = 5° 09' Dl = 16°,5. Очевидно, что затмение Солнца возможно и по другую сторону лунного узла, на таком же расстоянии от него. Дугу эклиптики в 33° Солнце, перемещаясь со средней скоростью 59' в сутки, проходит за 34 дня. Но за 34 дня обязательно будет одно новолуние, а может быть и два, так как продолжительность синодического месяца 29,5 суток. Следовательно, каждый год обязательно бывает 2 солнечных затмения (около двух узлов лунной орбиты), но может быть 4 и даже 5 затмений. Пять солнечных затмений в году случается тогда, когда первое происходит вскоре после 1-го января. Тогда второе наступает в следующее новолуние, третье и четвертое произойдут несколько раньше, чем через полгода, а пятое — через 354 дня после первого (через 354 дня пройдет 12 синодических месяцев).

Пусть теперь (рис. 63) С будет центр земной тени, угловой радиус которой на среднем расстоянии Луны равен 41'; L'L' — часть орбиты Луны, по которой движется центр Луны L, имеющий угловой радиус 15,5; < — восходящий узел лунной орбиты.

Для наступления лунного затмения необходимо, чтобы в полнолуние расстояние между центрами земной тени и Луны было меньше, чем 41' + 15',5 = 56',5. Из сферического прямоугольного треугольника CL < имеем

sin CL = sin С< sin Ð С<L

или

sin 56', 5 = sin С <, sin 5° 09',

откуда получаем

С< = Dl = 10°,6.

Следовательно, лунное затмение, хотя бы и непродолжительное, возможно в том случае, если центр земной тени отстоит от лунного узла, по одну или другую сторону, менее чем на 10°,6. Тень Земли, перемещаясь по эклиптике со скоростью 59' в сутки, проходит это расстояние за 10,8 суток, а двойное расстояние в 21°,2 — за 21,6 суток. Но так как синодический месяц содержит 29,5 суток, то одно полнолуние может произойти на расстоянии, большем 10°,6 к западу от узла, а следующее полнолуние — на таком же расстоянии к востоку от узла, и тогда в этом месяце лунных затмений не будет. Тем более их не будет и в следующий месяц, так как центр Луны пройдет через узел спустя 27,2 дня (драконический месяц), а полунолуние случится на 2,3 дня позже. За 2,3 дня Луна уйдет от узла на 30°, и центр ее пройдет мимо центра земной тени на расстоянии, большем 56’,5.

Следующее лунное затмение может произойти лишь через полгода, вблизи другого узла лунной орбиты, но по тем же причинам его может и не быть.

Таким образом, на протяжении года может не произойти ни одного лунного затмения, а самое большее их может быть два или три. Три лунных затмения в году случаются тогда, когда первое из них происходит вскоре после 1-го января, второе — в конце июня, а третье — в конце декабря, через 12 синодических месяцев (через 354 дня) после первого.