§ 95.
Универсальный
инструмент
Одним
из основных
угломерных
инструментов,
позволяющим
в любой точке
земной поверхности
измерить
горизонтальные
координаты
светила,
является универсальный
инструмент (рис.
70), который
состоит из
небольшой
астрономической
трубы,
имеющей
возможность
поворачиваться
вокруг двух
взаимно
перпендикулярных осей — горизонтальной и
вертикальной.
Установка
осей в
плоскости
математического
горизонта и в
вертикальной
плоскости производится
с помощью
уровней и
регулировочных
винтов.

Углы
поворота
трубы около
той и другой
оси отсчитываются
по двум
кругам или лимбам
— вертикальному
и
горизонтальному.
Вертикальный
круг
соединен с
горизонтальной
осью и служит
для отсчетов
углов в
вертикальной
плоскости;
горизонтальный
круг соединен
с
вертикальной
осью и по
нему
отсчитываются
углы в
горизонтальной
плоскости.
Круги делятся штрихами на градусы, а каждый градус — на 2, 3, 6 или 12 частей, т.е. между двумя соседними штрихами содержится 30', 20', 10' или 5'. Обычно 10-градусные, а иногда и 5-градусные штрихи оцифровываются.
Отсчеты каждого лимба производятся с помощью концентрического с ним круга, или части круга, на котором наносится нулевой штрих (указатель) для отсчета целых делений лимба.
Для
отсчета
долей
деления
лимба служит верньер
или нониус,
позволяющий
отсчитывать
углы с
точностью до
30", 20", 10" или 5",
смотря по
устройству
верньера.
Все отсчеты производятся сквозь лупу, а иногда и в микроскоп, так как деления кругов очень мелки.
Если
центр лимба
не совпадает
с центром оси
вращения, то
отсчет по
одному
верньеру
будет ошибочен.
Эта ошибка в
отсчете
называется ошибкой
эксцентриситета.
Она
исключается
при отсчетах
лимба в двух диаметрально
противоположных
точках круга,
из которых
берется
среднее
арифметическое.
Поэтому все
угломерные
инструменты
имеют по два
верньера для
каждого лимба.
В
идеальном
инструменте
вертикальная
и горизонтальная
оси должны
быть взаимно
перпендикулярны,
визирная
линия
перпендикулярна
к
горизонтальной
оси, а центры
осей вращения
должны
проходить
точно через
центры
разделенных
кругов. Но
идеальных
инструментов
не бывает.
Поэтому
одной из важнейших
задач
практической
астрономии
является
изучение
всех ошибок
инструментов
и разработка
методов их
исключения из
результатов
наблюдений,
или учета их
влияния на
измеряемые
величины. В
дальнейшем
мы будем считать
инструменты
безошибочными,
что равносильно
тому, что их
инструментальные
ошибки
учтены.
Универсальные
инструменты
изготовляются
сравнительно
небольших
размеров.
Диаметры
разделенных
кругов
находятся в
пределах от 10
до 30 см, а
фокусные
расстояния
их труб — от 10 до
50 см.
Если
в
универсальном
инструменте
вертикальный
круг
разделен
более точно,
чем горизонтальный,
то такой
инструмент
называется вертикальным
кругом. Если
горизонтальный
круг
разделен
точнее вертикального,
то
инструмент
называется теодолитом.
Последний
употребляется
главным
образом в
геодезических
работах при
измерении горизонтальных
углов.
Универсальный
инструмент
употребляется
почти
исключительно
как
переносный в
различного
рода
экспедициях
для определения
главным
образом
географических
координат
места
наблюдения (l и j ) и азимутов
земных
предметов.
Если
универсальный
инструмент
безошибочен
и с помощью
уровней
установлен
так, что его
горизонтальная
ось
находится в
плоскости
математического
горизонта, то
при вращении
трубы вокруг
этой оси
визирная
линия трубы
будет
поворачиваться
в
вертикальной
плоскости.
Обозначим
отсчет
вертикального
круга при
направлении
трубы в зенит
через Z0. Этот отсчет
называется местом
нуля круга,
или местом
зенита. Для определения
места зенита
надо
направить трубу,
при
положении
вертикального
круга справа
(или слева) от
нее, на
неподвижный
отдаленный
предмет, на
некоторой
высоте над горизонтом.
Записав
отсчет
вертикального
круга КП
(или КЛ ),
надо
повернуть
трубу вокруг
вертикальной
оси на 180°, затем
повернуть ее
вокруг
горизонтальной
оси и снова
направить на
тот же предмет,
и произвести
отсчет
вертикального
круга КЛ
(или КП).
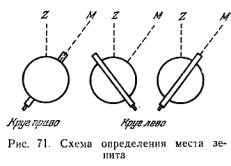
Легко
видеть (рис. 71),
что разность
отсчетов КП
— КЛ (или КЛ — КП,
смотря по
тому, в каком
направлении
оцифрован
круг) равна
удвоенному
зенитному
расстоянию
предмета, т.е. 2z. Тогда
|
|
(6.16) |
а место
зенита на
круге
|
|
(6.17) |
Из этих
двух формул
следует:
|
z = ± (Z0 — КЛ) |
(6.18) |
или
|
z = ± (KП — Z0). |
(6.19) |
При
наблюдениях
светил,
зенитные
расстояния
которых
непрерывно
меняются,
пользоваться
формулой (6,16)
нельзя, так
как отсчеты КП
и КЛ
делаются в
разные
моменты времени.
Зенитные
расстояния
светил определяются
по формуле (6.18)
или (6.19), если Z0 заранее
определено
по земному
предмету.
Поворотом
вертикального
круга на оси
можно
добиться
такого его
положения,
что Z0
будет близко
к нулю, и
тогда отсчет
круга даст сразу
зенитное
расстояние
любого
предмета. Но
сделать это с
точностью до
1 невозможно, и
при
высокоточных
измерениях
применяется
описанный
выше способ
измерения
зенитных
расстояний с
предварительным
определением
точного
значения
места зенита Z0 .
При наведении трубы на какой-либо предмет отсчет на горизонтальном круге будет указывать положение круга высоты этого предмета. Наведя трубу на второй предмет и отсчитав показание горизонтального круга, мы получим положение круга высоты второго предмета. Поэтому разность двух отсчетов горизонтального круга равна разности азимутов этих двух предметов. Для определения же азимута какого-либо предмета необходимо знать отсчет горизонтального круга при положении тpyбы в плоскости небесного меридиана (см. § 88).