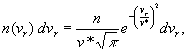§ 104. Некоторые сведения из молекулярной физики

Идеальный газ. Большинство астрономических объектов состоит из газа, который можно рассматривать как идеальный, так что справедливо основное уравнение состояния

(7.9)

В этой формуле р — внутреннее давление газа, r — его плотность, m — молекулярный вес газа, Т — его абсолютная температура, R = 8,32×10⁷ эрг/град× моль — универсальная газовая постоянная.

Как известно, отдельные молекулы, из которых состоит вещество, находятся в беспорядочном тепловом движении. Если молекула, имеющая массу т, движется со скоростью v , то ее кинетическая энергия равна

(7.10)

Тепловая энергия тела складывается из кинетической энергии всех его молекул. Из-за частых столкновений, скорости, а вместе с ними и кинетическая энергия тепловых движений отдельных молекул постоянно меняются. Однако можно говорить о величине тепловой энергии, которая в каждый данный момент в среднем приходится на одну частицу. Величина, характеризующая тепловое состояние тела и пропорциональная средней кинетической энергии, приходящейся на одну частицу, называется температурой. Если температуру измерять в Кельвинах, а энергию в системе СГС (эрг), то средняя энергия, приходящаяся на одну молекулу газа, составляет

(7.11)

Здесь k = 1,38 × 10^-16 эрг/К — постоянная Больцмана. Она представляет собой универсальную газовую постоянную R, но рассчитанную не на 1 моль, а на одну молекулу, т.е.

(7.12)

Величина k имеет очень важный физический смысл. Мы не можем сказать, сколько молекул газа в данный момент обладает каким-либо определенным значением энергии, потому что это зависит от их случайных столкновений. Однако мы можем сказать, какова вероятность того, что их энергия близка к такому-то значению. Оказывается, что k — это рассчитанная на 1°К наиболее вероятная энергия одной молекулы. Следовательно, при температуре Т большинство молекул газа должно иметь энергию близкую к величине kT. Если эта энергия равна 1 эв, то температура газа составляет

(7.13)

Энергию, отличающуюся от kT в ту или другую сторону больше чем в 2 раза, имеет меньше половины числа молекул, находящихся в некотором объеме газа. Вообще число частиц, имеющих энергию в пределах от e до e + De , быстро убывает по мере увеличения абсолютной величины разности | kT — e | . То же самое имеет место, если рассматривать вместо энергии частиц их скорости. Однако в этом случае следует учитывать, что движения частиц различаются также направлением.

Рассмотрим молекулу, обладающую наиболее вероятным значением кинетической энергии kT. Она должна двигаться с наиболее вероятной скоростью, равной по абсолютной величине

(7.14)

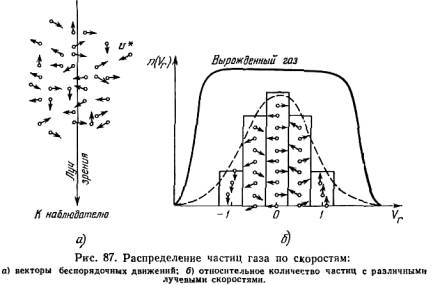
Предположим, что все молекулы в среднем движутся со скоростями, равными по величине v* . Тогда, поскольку их движения хаотичны, векторы скоростей отдельных молекул должны иметь всевозможные направления (рис. 87, а). В частности, по отношению к наблюдателю, который смотрит на газ со стороны, одна половина общего числа молекул должна в данный момент приближаться к нему, а другая — удаляться от него. Значительная доля молекул должна двигаться в плоскостях, близких к плоскости, перпендикулярной к лучу зрения. Эти молекулы почти не имеют составляющей скорости вдоль луча зрения, и их количество значительно больше числа молекул, движущихся вдоль луча зрения (рис. 87, 6). Если теперь учесть, что скорости молекул неодинаковы не только по направлениям, но и по величине, то оказывается, что число частиц, у которых составляющая скорости вдоль луча зрения заключена в пределах от v_г до v_r + dv_r , пропорционально экспоненте так что

(7.15)

где е = 2,718... — основание натуральных логарифмов, а п — общее число молекул в 1 см². Это — закон распределения Максвелла.

Для приближенного решения многих астрономических задач можно исходить из предположения, что все частицы имеют одинаковые энергии, равные kT, и в среднем движутся с одинаковыми по величине наиболее вероятными скоростями v* , определяемыми соотношением (7.14). Они очень близки к среднеквадратичной скорости

(7.16)

которую имеет молекула, обладающая средним для всех частиц значением энергии

Вырожденный газ. При увеличении числа частиц в идеальном газе их распределение по скоростям сохраняет форму прерывистой кривой на рис. 87, б. Растет только площадь, ограничиваемая этой кривой: она пропорциональна полному числу частиц. Однако когда количество частиц в заданном интервале скоростей оказывается слишком большим, наступает ограничение, накладываемое законами квантовой механики, называемое вырождением. Оно связано с тем, что импульсы частиц могут принимать только дискретные значения, а слишком близких частиц с одинаковыми импульсами быть не может (принцип Паули). Поэтому начиная с некоторых значений плотности (при T = 10⁷ °K это 10³ г/см³), дальнейшее ее увеличение происходит за счет пополнения области более быстрых частиц. При полном вырождении распределение становится плоским (сплошная кривая на рис. 87,6). Тем самым суммарный импульс единицы объема (т.е. давление) перестает зависеть от температуры и определяется только концентрацией частиц (т.е. плотностью). Скорость частиц, следовательно, также растет с плотностью. В квантовой статистике для уравнения состояния вырожденного газа вместо формулы (7.9) получается зависимость Р ~ r ^5/3.

Понятие об элементарных процессах. В астрофизике особое значение имеет анализ так называемых элементарных процессов, связанных с изменением энергии атомов, позволяющий установить зависимость между тепловой энергией газа и его излучением. Прежде всего важно знать, как часто сталкиваются между собой частицы газа. Сначала рассмотрим упрощенный случай: движется одна большая молекула, имеющая вид шарика с поперечным сечением s , а все остальные можно считать неподвижными точками. Пусть при этом взаимодействия происходят всякий раз, когда на пути большой молекулы. встречается какая-нибудь другая. Тогда она может двигаться без столкновения только до тех пор, пока не пройдет свободного объема, приходящегося на одну частицу. Если концентрация молекул п частиц/см³, то на каждую из них в среднем приходится объем пространства см³. Частица с поперечным сечением s, двигаясь со скоростью v*, пройдет такой объем за время

(7.17)

Это дает средний промежуток времени между двумя последовательными столкновениями. Обратная величина показывает, сколько столкновений происходит в среднем за 1 сек, и называется частотой столкновений

N = nv*s .

(7.18)

Путь, проходимый частицей между последовательными столкновениями, называется длиной свободного пробега, которая, очевидно, равна

(7.19)

Так как остальные частицы в среднем тоже имеют поперечники s , а площадь пропорциональна квадрату радиуса, то вместо s в выведенные формулы надо подставить величину в 4 раза большую. Кроме того, учет движений всех частиц, если они одинаковы, дает увеличение еще в раз.

Однако мы не будем вводить этих уточнений в полученные выше формулы, так как гораздо существеннее, что для микрочастиц (атомы, ионы, свободные электроны) представление о геометрических размерах вообще теряет смысл. Поэтому формулы (7.17)-(7.19) имеют смысл только в том случае, если под величиной а понимать лишь некоторый параметр, характеризующий вероятность того, что произойдет сближение рассматриваемых частиц, которое завершится данным явлением. Таким явлением может, например, быть упругое столкновение с простым перераспределением кинетической энергии, или столкновение, при котором определенным образом произойдет изменение внутренней энергии молекулы или атома и т.д. Как мы видим, этот параметр имеет размерность площади и потому называется эффективным сечением. Он показывает, что в данном процессе рассматриваемая частица ведет себя так же, как если бы она имела геометрический поперечник s, а частицы, с которыми она взаимодействует, — были бы неподвижными точками.

Так, например, для столкновений молекул в воздухе при обычных условиях эффективное сечение около 10^-14 см². Свободные электроны в газе при высоких температурах, сталкиваясь с нейтральными атомами, могут отрывать от них электроны (ионизовать). Эффективное сечение этого процесса при температуре 10 000° для водорода порядка 10^-16 см². Встретив ионизованный атом, свободный электрон может быть захвачен им и вернуться на прежнее место (рекомбинация). Для этого процесса эффективное сечение при тех же значениях температуры порядка 10^-21 см².

Чтобы пользоваться формулами (7.17)-(7.19), надо предварительно по формуле (7.14) вычислить наиболее вероятную скорость v*, которую имеет рассматриваемая частица при данной температуре. Молекулы воздуха движутся в среднем со скоростью 400 м/сек, а водородные атомы при температуре 10 000 °K — со скоростью около 10 км/сек. Средняя энергия частиц одинакова. Поэтому более легкие свободные электроны движутся в 37 раз быстрее атомов водорода.

При нормальных условиях в воздухе столкновения очень часты (около десяти миллиардов в секунду), а длина свободного пробега составляет сотые доли микрона. Однако в некоторых космических условиях, например, во внешних слоях атмосфер звезд, длина свободного пробега значительно больше и может достигать сантиметров, а в туманностях газ настолько разрежен, что столкновения частиц могут происходить раз в десятки и сотни лет. За это время частицы успевают совершить огромные пробеги в десятки астрономических единиц.