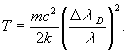§ 107. Доплеровское смещение спектральных линий

Если расстояние между излучающим телом и наблюдателем меняется, то скорость их относительного движения имеет составляющую вдоль луча зрения, называемую лучевой скоростью. По линейчатым спектрам лучевые скорости могут быть измерены на основании эффекта Доплера, заключающегося в смещении спектральных линий на величину, пропорциональную лучевой скорости, вне зависимости от удаленности источника излучения. При этом, если расстояние увеличивается (лучевая скорость положительна), то смещение линий происходит в красную сторону, а в противном случае — в синюю.

Объяснить это явление можно на основании следующих элементарных рассуждений. Вообразим наблюдателя, воспринимающего от объекта луч света. Предположим, что этот луч представляет собой отдельное непрерывное электромагнитное колебание (цуг волн). Пусть за 1 сек источник излучает n волн длиной l каждая. Так как n — частота, то . Неподвижный относительно источника наблюдатель за ту же одну секунду воспримет столько же (т.е. n ) волн. Теперь пусть источник или наблюдатель движутся с относительной скоростью v_r . Тогда по отношению к неподвижному цугу волн наблюдатель за 1 сек пройдет расстояние v_r , на котором укладывается волн. Таким образом, в случае движения вдоль луча зрения наблюдатель воспримет не n волн, а на меньше, если расстояние увеличивается, и на больше, если оно уменьшается. Следовательно, изменится частота наблюдаемого излучения n . Обозначая это изменение частоты через Dn и принимая, что положительным значениям v_r соответствует увеличение расстояния, получим

Учитывая зависимость между n и l , мы видим, что при движении вдоль луча зрения изменяется не только частота воспринимаемого излучения, но и длина его волны соответственно на величину

Объединяя это выражение с предыдущим, найдем окончательную формулу для величины доплеровского смещения спектральных линий

(7.40)

Более строгий вывод формулы для доплеровского смещения требует применения теории относительности. При этом получается выражение, которое при v_r << с очень мало отличается от формулы (7.40). Кроме того, оказывается, что смещение спектральных линий вызывается не только движениями вдоль луча зрения, но и перпендикулярными к нему перемещениями (так называемый поперечный эффект Доплера). Однако он, как и релятивистская поправка к формуле (7.40), пропорционален и должен приниматься во внимание только при скоростях, близких к скорости света.

Эффект Доплера играет исключительно важную роль в астрофизике, так как позволяет на основании измерения положения спектральных линий судить о движениях небесных тел. Приведем несколько примеров.

Вследствие обращения Земли вокруг Солнца ее скорость, по абсолютной величине близкая к v = 30 км/сек = 3×10⁶ см/сек, все время меняет свое направление в пространстве. Поэтому линии в спектрах звезд, к которым в данный момент направлено движение Земли, слегка смещены в фиолетовую сторону на величину Dl , причем

Для зеленой линии с l = 5000 Å = 5×10^-5 см смещение составляет 0,5 Å, что легко может быть измерено. Вектор скорости годичного движения Земли лежит в плоскости эклиптики и перпендикулярен к направлению на Солнце. Поэтому наибольшее смещение спектральных линий бывает в спектрах звезд, расположенных вблизи эклиптики на расстоянии 90° от Солнца. Поскольку обращение Земли происходит против часовой стрелки, если смотреть с северного полюса эклиптики, то в точке, расположенной на 90° к востоку, линии смещены к красному концу, а в противоположной точке — к фиолетовому.

У звезд, находящихся во всех остальных точках небесной сферы, смещение линий в спектрах звезд, вызванное годичным движением Земли, меньше. Оно в точности равно нулю для звезд, находящихся в полюсе эклиптики и в направлениях к Солнцу и от него. Смещение спектральных линий, вызванное суточным вращением Земли, линейная скорость которого на экваторе не превышает 0,5 км/сек, значительно меньше (самое большее тысячные доли ангстрема).

Для измерения смещения спектральных линий рядом со спектром исследуемого объекта, например звезды, на ту же пластинку фотографируют спектр лабораторного источника, в котором имеются известные спектральные линии. Затем при помощи микроскопов, снабженных точными микрометрами, измеряют смещение линий объекта по отношению к лабораторной системе длин волн и тем самым находят величину Dl , а по формуле (7.40) вычисляют лучевую скорость v_r . Если из этой скорости вычесть проекцию на луч зрения скорости годичного движения Земли, то получим лучевую скорость звезды относительно Солнечной системы.

Принцип Доплера позволяет не только судить о движении излучающего тела, но и о его вращении. Так, например, вследствие вращения Солнца восточный его край приближается к нам, а западный — удаляется. Наибольшая линейная скорость (на солнечном экваторе) достигает почти 2 км/сек, что при l = 5000 Å соответствует доплеровскому смещению Dl = 0,035 Å. По мере приближения к центру и полюсам солнечного диска лучевая скорость, а вместе с нею и доплеровское смещение уменьшаются до нуля. У звезд не удается наблюдать излучения отдельных частей их поверхности. Наблюдаемый спектр звезды получается в результате наложения друг на друга спектров всех точек ее диска, каждая из которых у вращающейся звезды дает различное смещение линий в спектре. В результате наблюдается расширение спектральных линий, на основании которого можно судить о величине линейной скорости вращения. У некоторых звезд линейные скорости вращения достигают огромных значений в сотни километров в секунду.

Даже в тех случаях, когда излучающий газ в целом не имеет относительного движения вдоль луча зрения, спектральные линии, излучаемые отдельными атомами, все равно имеют доплеровские смещения из-за беспорядочных тепловых движения. Поскольку в каждый момент множество атомов приближается к нам со всевозможными скоростями и примерно столько -же их удаляется с такими же скоростями, происходит симметричное расширение спектральной линии, изображенное на рис. 90. Такой график, показывающий распределение энергии, излучаемой в узкой области спектра в пределах спектральной линии, называется ее профилем. Если расширение линии вызвано только тепловыми движениями излучающих атомов, то по ширине профиля можно судить о температуре светящегося газа. Действительно, как указывалось в § 104, число частиц, обладающих различными скоростями вдоль луча зрения v_r , убывает с ростом | v_r |, по закону Вместе с тем, чем больше | v_r | , тем дальше в крыле линии излучает данный атом. При v_r > 0 излучение происходит в красном крыле, а при v_r < 0 — в синем. Если газ прозрачен к излучению в рассматриваемой линии (т.е. самопоглощение отсутствует) и, следовательно, интенсивность в каждой точке профиля пропорциональна количеству атомов, обладающих соответствующим значением v_r , то профиль спектральной линии повторяет закон распределения атомов по скоростям (7.15) и кривая, изображенная на рис. 90, представляется формулой

(7.41)

Из формулы (7.15) видно, что число частиц со скоростью v_r = v* в е раз меньше, чем частиц со скоростью v_r = 0. Эти атомы создают излучение в точке профиля линии, интенсивность I в которой в e раз меньше центральной I₀. Половина расстояния между точками профиля линии, в которых интенсивность составляет 1/е (37%) от центральной, называется доплеровской шириной спектральной линии Dl _D . Поскольку атомы, излучающие спектральную линию, смещенную на величину Dl _D , должны двигаться с наиболее вероятной скоростью v*, имеем

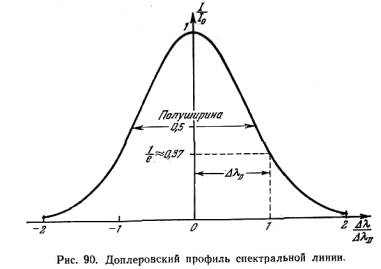
Если эта скорость обусловлена только тепловыми движениями, то, учитывая формулу (7.14), получим

(7.42)

Откуда

(7.43)

Если помимо тепловых движений в газе наблюдаются течения или какие-нибудь другие крупномасштабные движения (например, турбулентность), то спектральная линия расширяется еще сильнее, а иногда разбивается на несколько линий, соответствующих различным потокам. Таким образом, изучая профили спектральных линий, можно судить как о температуре, так и о движениях, происходящих в излучающем газе.