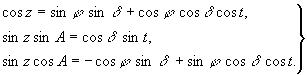§ 29. Параллактический треугольник и преобразование координат

Параллактическим треугольником называется треугольник на небесной сфере, образованный пересечением небесного меридиана, вертикального круга и часового круга светила. Его вершинами являются полюс мира Р, зенит Z и светило М.

Если светило М находится в западной половине небесной сферы (рис. 16), то сторона ZP

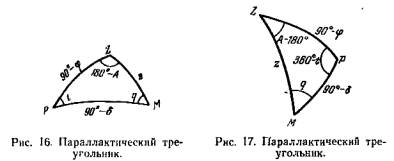
(дуга небесного меридиана) равна 90° — j , где j — широта места наблюдения; сторона ZM (дуга вертикального круга) равна зенитному расстоянию светила z = 90° — h, где h — высота светила; сторона РМ (дуга часового круга) равна полярному расстоянию светила р = 90° — d , где d — склонение светила; угол PZM = 180° — А, где A — азимут светила; угол ZPM = t, т.е. часовому углу светила; угол PMZ = q называется параллактическим углом.

Если светило находится в восточной половине небесной сферы (рис. 17), то значения сторон параллактического треугольника те же, что и в случае пребывания светила в западной половине, но значения углов при вершинах Z и Р иные, а именно: угол PZM = А — 180°, а угол ZPM = 360° — t .

Вид параллактического треугольника для одного и того же светила зависит от широты места наблюдения j (от взаимного расположения Р и Z) и от момента наблюдения, т.е. от часового угла t.

Применяя основные формулы сферической тригонометрии к параллактическому треугольнику (рис. 16) и считая исходными сторону РМ и угол t, получим

cos (90° — d ) = cos (90° — j ) cos z + sin (90° — j ) sin z cos (180° — A),

sin (90° — d ) sin t = sin z sin (180° — A),

sin (90° — d ) cos t = sin (90°— j ) cos z — cos (90° — j ) sin z cos (180° — A)

или

(1.36)

Формулы (1.36) служат для вычисления склонения светила d и его часового угла t (а затем и прямого восхождения a = s — t) по измеренным (или известным) его зенитному расстоянию z и азимуту A в момент звездного времени s). Иными словами, они служат для перехода от горизонтальных координат светила к его экваториальным координатам.

Если исходными считать сторону ZM = z и угол 180° — A, то основные формулы в применении к параллактическому треугольнику напишутся в следующем виде:

cos z = cos (90° — j ) cos (90° — d ) + sin (90° — j ) sin (90° — d ) cos t,

sin z sin (180° — A) = sin (90° — d ) sin t,

sin z cos (180° — A) = sin (90° — j ) cos (90° — d ) — cos (90° — j ) sin (90° — d ) cos t

или

(1.37)

Формулы (1.37) служат для вычисления зенитного расстояния z и азимута светила A (для любого момента звездного времени s и для любой широты j ) по известному склонению светила d и его часовому углу t = s — a . Иными словами, они служат для перехода от экваториальных координат светила к его горизонтальным координатам.

Кроме того, формулы (1.36) и (1.37) используются при вычислении моментов времени восхода и захода светил и их азимутов в эти моменты, а также при решении двух очень важных задач практической астрономии — определения географической широты места наблюдения j и определения местного звездного времени s.

Для перехода от экваториальных координат светила (a и d ) к его эклиптическим координатам (l и b ) и наоборот можно вывести формулы, аналогичные формулам (1.36) и (1.37). Только в этом случае надо основные формулы § 28 применить к сферическому треугольнику небесной сферы, вершинами которого являются полюс мира Р, полюс эклиптики П и светило М, а стороны и углы имеют значения, указанные на рис. 18.