§ 50. Второй закон Кеплера

Возьмем прямоугольную систему координат, начало которой находится в центре притяжения, а плоскость ху совпадает с плоскостью орбиты тела.

Проектируя ускорение и силу на координатные оси х и у (рис. 31), напишем основное уравнение динамики (2.14) в следующем виде:

Умножая эти уравнения соответственно на у и х и вычитая первое из второго, получим

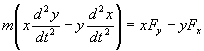
или

Поскольку сила центральная, то имеет место соотношение

Поэтому

или

(2.21)

В полярных координатах

х = r cos q, у = r sin q,

где r — расстояние точки от начала координат (радиус-вектор точки), а q — полярный угол (истинная аномалия).

Если перейти от прямоугольной системы координат к полярным координатам, то выражение (2.21) будет иметь вид

(2.22)

т.e. площадь, описанная радиусом-вектором за единицу времени, есть величина постоянная. Это есть математическое выражение второго закона Кеплера (см. § 40).