§ 61. Определение радиуса Земли. Триангуляция

Согласно теории всемирного тяготения всякое массивное, изолированное тело, вращающееся вокруг оси с определенной скоростью (не очень быстро), должно принять форму, близкую к шару. Действительно, все наблюдаемые массивные небесные тела (Солнце, Луна, планеты) имеют формы, мало отличающиеся от правильных шаров. Шарообразность Земли хорошо видна на ее фотографиях, полученных из космоса (1967-1969 гг.).

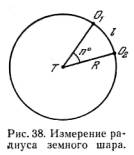
Шарообразность Земли позволяет определить ее размеры способом, который был впервые применен еще Эратосфеном в III в. до н. э. Идея этого способа проста. Возьмем на земном шаре две точки O₁ и О₂ , лежащие на одном географическом меридиане (рис. 38). Обозначим длину дуги меридиана O₁O₂ (например, в километрах) через l, а ее угловое значение (например, в градусах) — через п°. Тогда длина дуги 1° меридиана l₀ будет равна а длина всей окружности меридиана где R — радиус земного шара. Отсюда

Угловое значение дуги п° равно разности географических широт точек O₁ и О₂, т.е. п° = j ₁ — j ₂ , определение которых представляет простую астрометрическую задачу (см. § 86, 87).

Значительно сложнее определить линейное расстояние l между точками O₁ и О₂. Непосредственное измерение расстояния по кратчайшей линии между этими точками, отстоящими одна от другой на сотни километров, невыполнимо вследствие естественных препятствий — гор, лесов, рек и т.п. Поэтому длина дуги l определяется путем вычислений с помощью специального способа, который требует непосредственного измерения только сравнительно небольшого расстояния — базиса и ряда углов. Этот способ разработан в геодезии и называется триангуляцией.

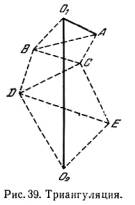
Суть метода триангуляции заключается в следующем. По обе стороны дуги O₁О₂ (рис. 39), длину которой необходимо определить, выбирается несколько точек А, В, С, ... на расстояниях 30-40 км одна от другой. Точки выбираются так, чтобы из каждой были видны по меньшей мере две другие точки. Во всех точках устанавливаются геодезические сигналы — вышки в форме пирамид — высотой в несколько десятков метров. Наверху сигнала устраивается площадка для наблюдателя и инструмента. Расстояние между какими-нибудь двумя точками, например O₁А , выбирается на совершенно ровной поверхности и принимается за базис. Длину базиса очень тщательно измеряют непосредственно с помощью специальных мерных лент. Наиболее точные современные измерения базиса длиной в 10 км производятся с ошибкой ±2 мм. Затем устанавливают угломерный инструмент (теодолит)

последовательно в точках O₁, A, В, С, ..., O₂ и измеряют все углы треугольников O₁АВ, АВС, BCD, ... Зная в треугольнике O₁AB все углы и сторону O₁A (базис), можно вычислить и две другие его стороны O₁B и АВ, я зная сторону АВ и все углы треугольника ABC. можно вычислить стороны АС и ВС и т.д. Иными словами, зная в зтой цепи треугольников только одну сторону (базис) и все углы, можно вычислить длину ломаной линии O₁BDO₂ (или O₁ACEO₂ ) . При этих вычислениях учитывается, что треугольники не плоские, а сферические. Далее, определив из точки O₁ азимут направления стороны O₁В (или O₁A), можно спроецировать ломаную линию O₁ВDO₂ (или O₁АСЕO₂ ) на меридиан O₁O₂ , т.е. получить длину дуги O₁O₂ в линейных мерах.