 of the
cosine is related to the
of the
cosine is related to the  wavelet duration
wavelet duration  by the relation
by the relation



The concepts of Fourier frequency and wavelet duration are obviously related. To translate results (e.g. spectra) from one to the other, the relation needs to be established at a quantitative level. The result is somewhat unsettling, because the correspondence will depend on the wavelet shape.
Among many sensible definitions, we chose to require that
the peak of the wavelet mean spectrum should be matched with
the singularity of the Fourier transform of the cosine wave.
Then, it can be shown that the frequency
 of the
cosine is related to the
of the
cosine is related to the  wavelet duration
wavelet duration  by the relation
by the relation
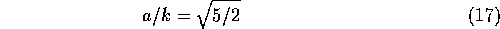
 wavelet
wavelet
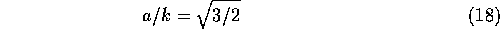
Analytically, the peak of the
The ambiguous definition of the duration of an event is common
to the sizing of any object of irregular shape. Say, if an object
is a perfect hard sphere, nobody will argue taking its diameter as
THE size (although its radius and circumference could also be
adopted). But what is the size of a spheroid, such as the Earth?
What is the size of a snowball? of a football? of a cotton ball?
A mean effective diameter might make sense if the total volume
occupied is the primary concern - but what if the mass of material
is (think of the cotton ball)? what if the spheroid is to fit
in a hole with tight tolerances?
Similarly, many definitions of `duration' (and an associated dominant
frequency) emerge from our analysis. Each wavelet shape will provide
a slightly different number, and should be used accordingly with
caution.
 mean wavelet spectrum is obtained
by cancelling the derivative of the spectrum with respect to k:
mean wavelet spectrum is obtained
by cancelling the derivative of the spectrum with respect to k:
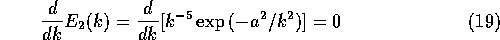



Jacques Lewalle
Mon Nov 13 10:51:25 EST 1995