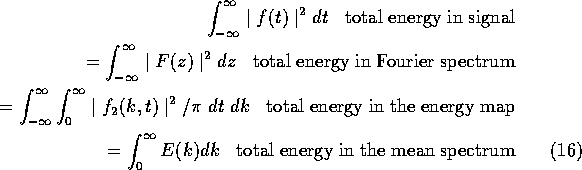



The content of the Parseval formulae for Fourier and wavelet transforms needs to be reexamined.
What the equations say is the following
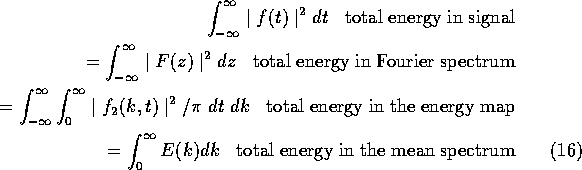
It is a matter of interpretation to associate the integrands with an energy density. By using the Fourier spectra exclusively, the user may have developed a false sense of security in this regard, and the clear interpretation in the case of periodic signals provides no hint of trouble. However, in the case of broadband spectra associated with a sequence of square waves, say, the particular spectral content at a given frequency is clearly an artifact of the sine wave decomposition. As the signal becomes more intermittent or modulated, no functional basis seems privileged, least of all a periodic one covering the entire time axis.
It takes some time and thought to get comfortable with the idea that the Fourier power spectrum is not the absolute answer to spectral energy distribution. In all cases, the Parseval theorem only guarantees that the integrals of the power spectrum over all frequencies/durations is the same: it is our prerogative to interprete the integrand as a spectral energy density, but it is our responsibility to do so with care.


