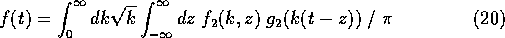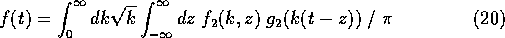



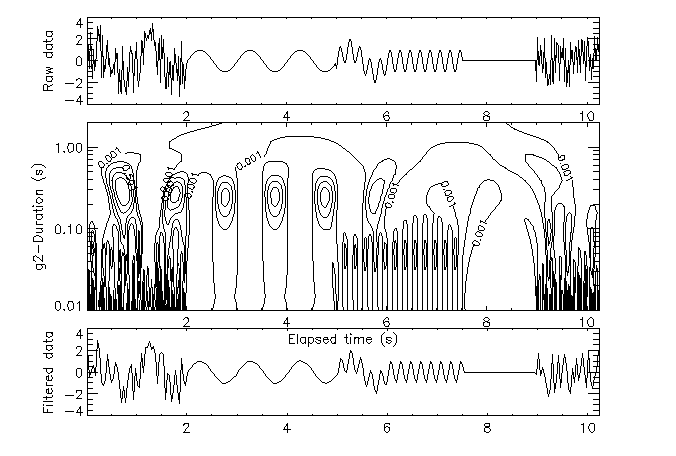
As in the case of Fourier transforms, the wavelet maps suggest that the signal is made of various contributions, and in fact that it may be reconstructed from the wavelet coefficients. Unfortunately, the value of the signal at one time is not a simple superposition of simultaneous values from one vertical line of the wavelet map: rather, contributions from the neighborhood of this time must be used. In fact, we have a convolution (at each duration) of the wavelet coefficients with the analyzing wavelet, followed by an integration over all durations. On the Fig. 15, we see that the signal is reconstructed faithfully, except in this particular case for the highest frequency part of the noise (a shortcoming that could be remedied by extending the wavelet map toward shorter durations).
Analytically, the inverse transform for the Mexhat is given by