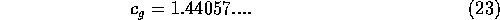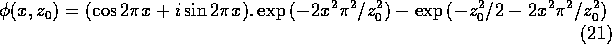
The Morlet wavelet is arguably the `original' wavelet. Although the discrete Haar wavelets predate Morlet's, it was only as a consequence of Morlet's work that the mathematical foundations of wavelets as a better formulation of time-frequency methods were laid.
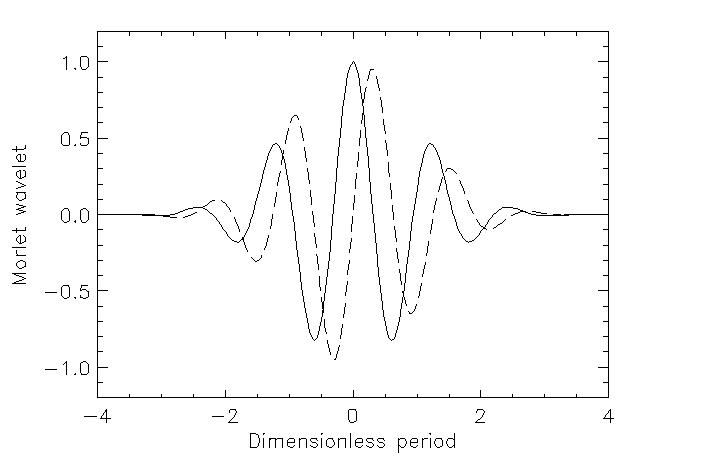
Conceptually related to windowed-Fourier analysis, the Morlet wavelet is a locally periodic wavetrain. It is obtained by taking a complex sine wave, and by localizing it with a Gaussian (bell-shaped) envelope (Fig. 16).
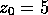
Analytically, a non-oscillatory function must be subtracted so that the admissibility condition is satisfied. For a sine wave of unit frequency inside an envelope of width z_0 / pi , we have
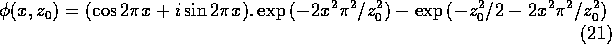
reflects a compromise between localization
in time (the Mexican hat isolates a single bump) and
in frequency (Fourier's infinite wavetrain pinpoints the
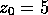frequency): the value is recommended in practice, but
can be modified.
Clearly, the wavelet transform will have a real and an imaginary part, and it is useful to represent them in `polar' coordinates: the norm is the magnitude of the transform and, being related to the local energy, is of primary interest, while the polar angle (phase) completes the representation. Just as in the case of a Fourier transform, both real and imaginary parts must be known in order to calculate an inverse transform and reconstruct the signal. Only the norm-transfrom will be shown below.
In order for the squared norm of the Morlet transform to measure the local spectral energy, it must be divided by the normalization factor
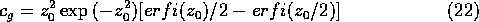
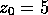used in the plots above,
