Morlet transform of modulated oscillations



Next: General formulae
Up: No Title
Previous: Morlet wavelet and
The modulated waves of section 14 are processed using the
Morlet wavelet, and their local norms are shown below.
For the 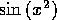 signal, the Morlet wavelet shows the continuous
shift toward high frequencies (Fig. 17) (Note: the ordinates should be
labeled `Period (s)'. I will redo these plots at some point).
The most striking difference with the Mexican-hat transform
in section 14 is the shift in emphasis from the individual maxima
and minima to the local periodicity.
signal, the Morlet wavelet shows the continuous
shift toward high frequencies (Fig. 17) (Note: the ordinates should be
labeled `Period (s)'. I will redo these plots at some point).
The most striking difference with the Mexican-hat transform
in section 14 is the shift in emphasis from the individual maxima
and minima to the local periodicity.

Figure 17: Morlet-wavelet transform of
the 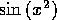 signal.
signal.
In the case of the amplitude/frequency modulated wave (Fig. 18), the results
are less clear than in the Mexican hat case, because no frequency
has time to get established and `resonate' with this particular
wavelet.
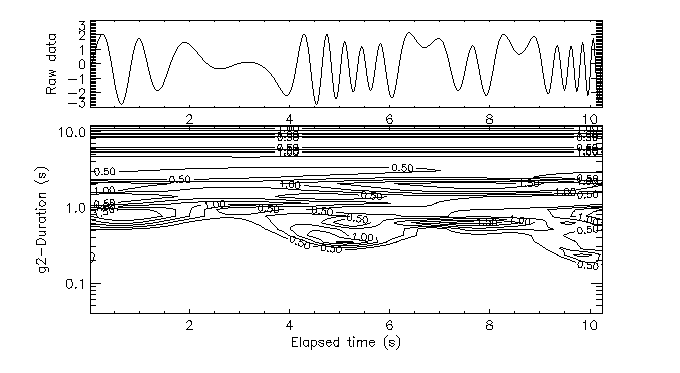
Figure 18: Morlet-wavelet transform of the modulated oscillation.
Finally, for the intermittent data, the Morlet wavelet (Fig. 19) establishes
a clear distinction between the random fluctuations and the
periodic patches. It is noteworthy that the period of the
sine waves is determined much more accurately than with the
Mexican hat: the compromise between spatial and spectral
localization is clearly demonstrated: Morlet favors spectral
accuracy while Mexican hat favors individual event localization.
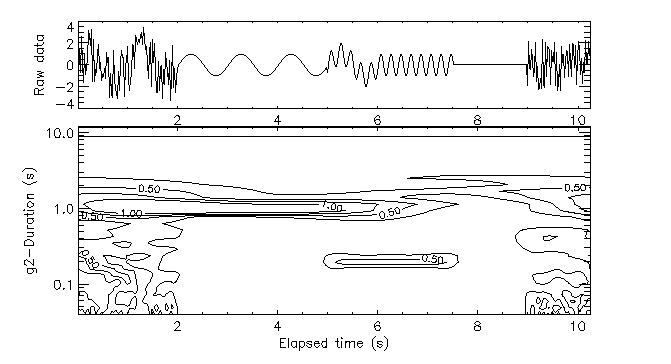
Figure 19: Morlet-wavelet transform of the intermittent signal.
Thus, the selection of the wavelet will be quite important, and
practice will guide the user to some standard wavelets. In all
instances, it will be important to interprete the results by
keeping in mind what different wavelets can and cannot do.



Jacques Lewalle
Mon Nov 13 10:51:25 EST 1995
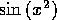 signal, the Morlet wavelet shows the continuous
shift toward high frequencies (Fig. 17) (Note: the ordinates should be
labeled `Period (s)'. I will redo these plots at some point).
The most striking difference with the Mexican-hat transform
in section 14 is the shift in emphasis from the individual maxima
and minima to the local periodicity.
signal, the Morlet wavelet shows the continuous
shift toward high frequencies (Fig. 17) (Note: the ordinates should be
labeled `Period (s)'. I will redo these plots at some point).
The most striking difference with the Mexican-hat transform
in section 14 is the shift in emphasis from the individual maxima
and minima to the local periodicity.





