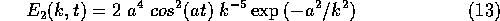Energy distribution

One of the most widely used tools of Fourier analysis is the Parseval theorem. It enables the experimentalist to view how the `energy' in the signal is distributed among frequencies. The Fast Fourier Transform (FFT) algorithms have made power spectra one of the obvious diagnostics tools during data acquisition, and energy maps are a versatile alternative.

Wavelet transforms are endowed with a similar theorem. This time, the energy density is distributed in the wavelet half-plane , according to the expression

for the Mexican hat transform (for other wavelets, the normalization constant is different: see below). The result is an energy map (Fig. 9), showing the distribution of energy corresponding to the wavelet map (Fig. 6).

Figure 9: Energy distribution in time/duration is wavelet dependent.

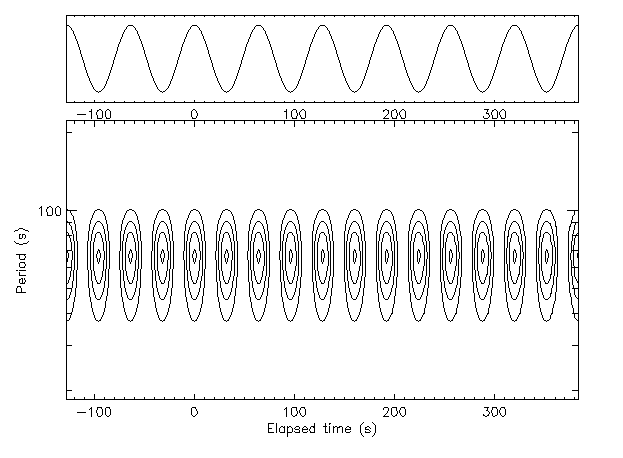
Analytically, of course,

for the Mexhat transform of the cosine.

Jacques Lewalle
Mon Nov 13 10:51:25 EST 1995