
The inverse transform is at the core of the best known applications of wavelets: data compaction and numerics. These applications concern themselves with how little information is necessary to reconstruct the signal with good accuracy. The reader interested in these topics should consult the voluminous literature on the subject.
The most economical representation is not our priority here: we would like to get a more thorough characterization of a complicated signal. Two applications fall within our scope: filtering and denoising.
Filtering consists of using only a portion of the wavelet map in the inverse transform process, masking out certain durations. This is easily done graphically (hide parts of the map), numerically (skip those durations) and analytically (integrate over a portion of the k-axis). The following plot (Fig. 23) was generated from the intermittent data, using only the a band of the wavelet map located between 20% and 40% from the top of the map.
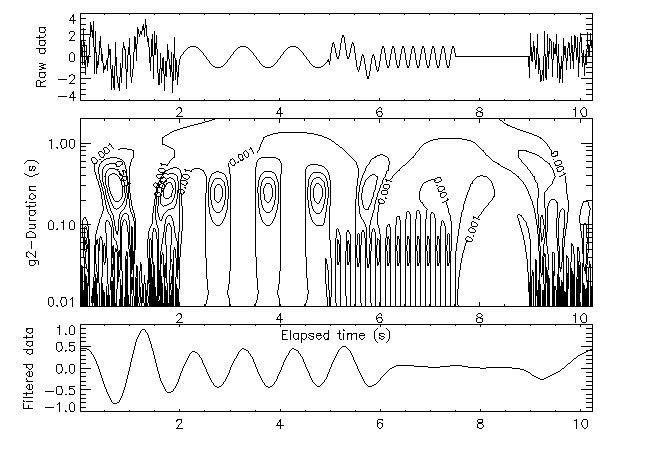
`Surgical' removal of events is also possible, and user judgement in constructing a relevant algorithm is very important.